最近开始对凸优化(convex optimization)中的ADMM(Alternating Direction Method of Multipliers)交替方向乘子算法开始感兴趣，接下来我会写一系列关于ADMM(Alternating Direction Method of Multipliers)交替方向乘子算法的内容。

凸优化：ADMM(Alternating Direction Method of Multipliers)交替方向乘子算法系列之二：Precursors

[本文地址：http://blog.csdn.net/shanglianlm/article/details/46808763]

2- 先导（Precursors）

2-1 对偶上升法（Dual Ascent）

设有如下优化问题：

$$\text{min} f(x) \ \ \ \text{s.t. } \ \ \ Ax = b \ \ \ \ \ \ \ \ \ \text{(2.1)}$$
它的拉格朗日形式为：
$$L(x, \lambda) = f(x) + \lambda^{T}(Ax - b)$$
对偶形式为：
$$g(\lambda) = \text{inf}_x L(x, \lambda) = -f^{*}(-A^{T}\lambda) - b^{T}\lambda$$
其中 f^* 是 f 的共轭函数。

The conjugate function

对偶问题为：

$$\text{max} \ g(\lambda)$$
假设强对偶成立，原问题和对偶问题的最优值一样（Assuming that strong duality holds, the optimal values of the primal and dual problems are the same）。

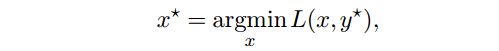
对偶上升法的迭代更新为：

$$x^{k+1} = \text{argmin}_{x}L(x, \lambda^{k}) \ \ \ \ \ \ \ \ \ \ \ \ \ \text{(2.2)}\ \ \ \ \text{x-最小化}$$ $$\lambda^{k+1} = \lambda^{k} + \alpha^{k}(Ax^{k+1} - b) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{(2.3)} \ \ \ \ \ \text{对偶变量更新}$$
其中 $\alpha^{k} > 0$是步长。

2-2 对偶分解法（Dual Decomposition）

假设目标函数是可以分解的，即

$$f(x) = \sum_{i=1}^{N}f_{i}(x_{i})$$
因此，拉格朗日函数可以改写为：
$$L(x, \lambda) = \sum_{i=1}^{N}L_{i}(x_{i}, \lambda) = \sum_{i=1}^{N}(f_{i}(x_{i}) + \lambda^{T}A_{i}x_{i} - (1/N)\lambda^{T}b)$$
所以它的迭代更新为：
$$x_{i}^{k+1} = \text{argmin}_{x_{i}}L_{i}(x_{i}, \lambda^{k}) \ \ \ \ \ \ \ \ \text{(2.4)}$$ $$\lambda^{k+1} = \lambda^{k} + \alpha^{k}(Ax^{k+1} - b) \ \ \ \ \ \ \ \ \text{(2.5)}$$

2-3 增广拉格朗日(Augmented Lagrangians)

为了增加对偶上升法的鲁棒性和放松函数 f 的强凸约束，我们引入增广拉格朗日(Augmented Lagrangians)形式：

$$L_{\rho}(x, \lambda) = f(x) + \lambda^{T}(Ax - b) + (\rho/2)||Ax - b||_{2}^{2}\ \ \ \ \ \ \ \ \text{(2.6)}$$
其中惩罚因子 $\rho>0$。
与 (2.1) 式相比，(2.6) 式只是增加了一个惩罚项。

2-4 乘子法(Method of Multipliers)

对应于的迭代公式为：

$$x^{k+1} = \text{argmin}_{x}L_{\rho}(x, \lambda^{k}) \ \ \ \ \ \ \ \ \text{(2.7)}$$ $$\lambda^{k+1} = \lambda^{k} + \rho(Ax^{k+1} - b) \ \ \ \ \ \ \ \ \text{(2.8)}$$
我们称之为乘子法(Method of Multipliers)。

将拉格朗日应用于对偶上升法可以极大地增加它的收敛属性，但是它要求一些代价。当 f 可以分解，而拉格朗日$L_{\rho}$不能分解的，因此 (13) 式不能对每个$x_{i}$并行最小化。这意味着乘子法不能被用来分解。于是我们引出ADMM （见 下节）。

参考或延伸材料：
[1]Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers
[2] 凸优化讲义
[3] A Note on the Alternating Direction Method of Multipliers