在机器学习的领域里，损失函数（Loss Function）如同一位严苛的导师，既为模型指引优化方向，又严格衡量其预测能力。本文将从定义、常见类型、优缺点到适用场景，为您全面解析这一核心概念。

        

1、什么是损失函数？

定义：损失函数是一种量化模型预测值与真实值之间差异的指标。它通过计算预测误差，将模型的“好坏”转化为一个数值，从而指导优化过程。
核心作用：

1. 模型评估：损失值越小，模型预测越接近真实值。
2. 参数优化：通过最小化损失函数调整模型参数，提升预测精度。
3. 反向传播驱动：计算梯度以更新模型权重，是深度学习的“引擎”。
4. 模型选择依据：不同任务需适配不同损失函数。

2、常见损失函数及数学形式 

2.1  均方误差（MSE）

数学公式：

特性分析：

• 优点：

  • 光滑可导，收敛速度快。

  • 计算简单，对大误差敏感，梯度平滑易优化。

  • 几何意义明确：最小化预测值与真实值的欧氏距离。

• 缺点：

  • 对异常值敏感，误差平方放大离群点影响。

  • 对离群点（Outliers）敏感，异常值可能导致梯度爆炸。

• 适用场景：

  • 数据分布均匀、无极端值的回归任务（如温度预测）。

  • 需严格惩罚大误差的场景（如金融风险评估）。

 2.2  平均绝对误差（MAE）

数学公式： 

特性分析：

• 优点：

  • 鲁棒性强，对异常值不敏感。

  • 梯度稳定。

  • 损失值与原始数据单位一致，解释性强。

•  缺点：

  • 梯度恒定导致收敛速度慢

• 适用场景：

  • 存在离群点的回归任务（如销售额预测）

 2.3  Huber损失

 数学公式： 

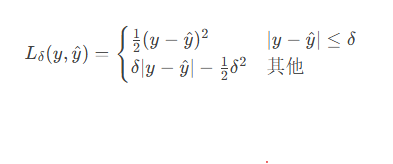
特性分析：

• 优点：

  • 结合MSE和MAE优点：小误差用平方项，大误差用线性项。

  • 对离群点鲁棒，梯度在极小值附近平滑。

•  缺点：

  • 需手动调整超参数δ，增加调参复杂度。

• 适用场景：

  • 噪声数据回归（如传感器数据预测）

  • 需平衡异常值影响与模型精度的场景。

 2.4  对数损失（Log Loss）

 数学公式： 

特性分析：

• 优点：

  • 直接优化分类概率，适用于概率输出模型（如逻辑回归）。

  • 对错误分类惩罚大，适合类别平衡的数据。

•  缺点：

  • 对类别不平衡数据敏感（如正负样本比例1:100时，模型易偏向多数类）。
  • 预测极端值时梯度不稳定。

• 适用场景：

  • 二分类任务需概率解释的场景（如信用评分模型）。

  • 类别平衡的分类任务（如医学图像中的肿瘤检测）。

 

 2.5  交叉熵损失（Cross-Entropy Loss）

 数学公式： 

特性分析：

• 优点：

  • 概率解释性强，梯度更新效率高。

  • 梯度随误差增大而显著，适合分类任务。

•  缺点：

  • 对预测极端值敏感（如预测概率接近0或1时梯度爆炸）。
  • 多分类任务中需配合Softmax使用，计算复杂度较高。

• 适用场景：

  • 多分类任务（图像识别、情感分析等）。

  • 二分类任务（如欺诈检测、广告点击率预测）。

 

 2.6  Hinge损失

 数学公式： 

特性分析：

• 优点：

  • Hinge损失通过惩罚分类错误和接近分类边界的样本，推动模型寻找最大间隔超平面，提升模型的泛化能力。

  • 与交叉熵等概率型损失不同，Hinge损失仅关注样本是否被正确分类，而非概率分布的细微变化，因此对标签噪声或异常值不敏感。

  • 在SVM中，Hinge损失与L2正则化结合时，能自动选择关键特征（支持向量），产生稀疏模型。

•  缺点：

  • Hinge损失在分类正确且置信度足够高时（即 y·f(x) ≥ 1），导数为0，可能导致梯度下降时跳过有效信息，训练初期收敛较慢。
  • 即使样本被正确分类但置信度低（如 0 < y·f(x) < 1），Hinge损失仍会产生惩罚，可能使模型在优化间隔时过度关注“容易样本”。
  • 在非线性问题中，需依赖核方法（如RBF核），但核函数选择和计算复杂度可能限制实用性。

• 适用场景：

  • 支持向量机（SVM）。

  • 二分类任务

  • 存在标签噪声或异常值的数据

  • 高维稀疏数据

3、选择策略与实践

1. 任务类型：
   • 回归任务：数据含离群点→Huber或MAE；需严格惩罚大误差→MSE。
   • 分类任务：多类别且概率敏感→交叉熵；二分类且需概率输出→对数损失。
2. 数据特性：
   • 含离群点：优先选择Huber或MAE避免梯度爆炸。
   • 类别不平衡：交叉熵配合类别加权（如Focal Loss）。
3. 模型类型：
   • 神经网络：默认交叉熵（分类）或MSE（回归）。
   • 树模型：常用MAE或MSE（对异常值敏感度低）。
4. 优化目标：
   • 快速收敛：MSE（梯度随误差减小而下降）。
   • 鲁棒性优先：MAE或Huber。

4、总结

损失函数是机器学习模型的“灵魂”，它不仅决定了模型的优化方向，还直接影响最终性能。在选择损失函数时，需综合考虑任务类型、数据特性及模型架构。通过合理设计损失函数，我们可以让模型在复杂的数据海洋中精准导航，最终抵达预测能力的彼岸。