连续变量的全概率和贝叶斯公式_人工智能导论——不确定性,概率推理和贝叶斯网络(一)...
不确定性能力无知:对问题本身的无知对理论知识的匮乏系统性能误差:在机器学习中称为“噪声”我们应该接受这种不确定性,在必要时候会利用它对不确定建模的时候,我们会使用:逻辑,模糊逻辑,概率概率和统计概率是纯数学问题,一定有唯一解统计不是纯数学问题,它的结论是多样性的概率空间:所有可能结果的集合Ω事件:概率空间Ω的子集概率公理:定义了概率函数P:Ω—>[0,1]非负性归一性可加性概率推理:不仅仅用
·
不确定性
- 能力
- 无知:
- 对问题本身的无知
- 对理论知识的匮乏
- 系统性能误差:在机器学习中称为“噪声”
- 我们应该接受这种不确定性,在必要时候会利用它
- 对不确定建模的时候,我们会使用:逻辑,模糊逻辑,概率
概率和统计
- 概率是纯数学问题,一定有唯一解
- 统计不是纯数学问题,它的结论是多样性的
- 概率空间:所有可能结果的集合Ω
- 事件:概率空间Ω的子集
- 概率公理:定义了概率函数P:Ω—>[0,1]
- 非负性
- 归一性
- 可加性
- 概率推理:不仅仅用公理,还会用一些定理(推理的中间结果)
- 分治的思想:将全联合概率分布拆分为若干小的条件分布或者无条件分布
- 在解决问题的过程中,我们可以先作独立性假设,该假设来自领域知识以及问题的复杂性;通过独立性假设来让问题简单化
- 先验独立性和条件独立性
- 先验独立性:P(X,Y) = P(X)*P(Y)
- 条件独立性:P(X,Y|Z) = P(X|Z)*P(Y|Z)或P(X|Y,Z) = P(X|Z)
- 补充:条件独立性比独立性更加常见
概率推理
- 例子:求解Query的概率分布
- 一般来说,我们将空间划分为Query,Evidence,Hidden三部分,复杂问题通常集合比较大

- 全联合概率分布的表示问题
- 玩具问题是低维全联合概率分布
- 所有变量是离散型:X1,X2,X3.......Xn
- 全联合概率分布:P(X1:n) = P(X1)*P(X2|X1)*........P(Xn|X1:n-1)(该公式并未将计算空间变小)
- 使用条件独立性简化(使用领域知识):将P(Xn|X1:n-1)中Xn只于前面一个变量有关,简化后得到一个贝叶斯网络

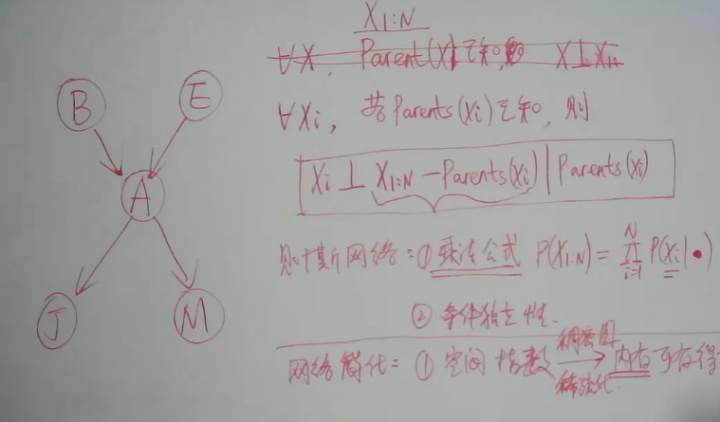
- 贝叶斯网络
- 有向无环图
- 结点表示随机变量,边为依赖关系
- X—>Y,表示Y依赖于X
- 贝叶斯网络使用条件独立性,把一个全连通图简化为一个稀疏的图,实际上就是用条件概率分布代替联合概率分布
- 一个结点独立于除了马尔可夫覆盖(父母+孩子+孩子的其他父母)之外的所有结点
- 推理
- 精确推理:先用条件独立性近似,再用乘法公式体现精确,计算复杂度高O(N*b^N)
- 不确定性推理:见贝叶斯网络笔记(二)
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)