本文是使用python实现简易的感知机模型, 用于进行sklearn库中的手写数字的简单分类(分为两类)

下面直接开始代码:

1. 导包

import numpy as np  # 进行矩阵运算和变换
from sklearn.datasets import load_digits  # 得到手写数字数据集
import matplotlib.pyplot as plt  # 进行acc变化曲线的绘制

2. 得到数据

# 得到数据
digits = load_digits()
# 特征空间
features = digits['data']

# 将数字 0~4 分类类别-1; 数字 5~9 分为类别2
labels = (digits['target'] > 4).astype(int) # 将大于 4 的标签转换为 1, 小于 4 的转换为 0
labels[labels == 0] = -1; # 将小于 4 的标签转换为 -1

digits数据集的简单介绍:

digits数据集键值对: ‘images’, ‘data’, ‘target’, ‘target_names’, ‘DESCR’

• images: ndarray类型, shape为(1797, 8, 8), 保存 8*8 的数值矩阵共1797个, 用来显示图片
• data: ndarray类型, shape为(1797, 64), 将 8*8 的矩阵按行展开成一行, 一行有64个属性值, 共有1797行,
• target: ndarray类型, shape为(1797,) , 指明每张图片代表的数字, 即标签
• target_names: ndarray类型, 数据集中所有标签值: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
• DESCR: 数据集的描述，作者，数据来源等

3. 打乱并划分数据集

shuffle_indices = np.random.permutation(features.shape[0])  
# 得到长度为数据个数并打乱顺序的数组, 来作为索引

features = features[shuffle_indices]  # 通过索引得到打乱后的特征和标签
labels = labels[shuffle_indices]

train_num = int(features.shape[0] * 0.8)  # 按照 8:1 划分数据集
train_datas, train_labels = features[:train_num, :], labels[: train_num]
test_datas, test_labels = features[train_num:, :], labels[train_num:]

# 输出数据形状
print(test_datas.shape, test_labels.shape)     # (360, 64) (360,)
print(train_datas.shape, train_labels.shape)   # (1437, 64) (1437,)

4. 定义超参数

BATCH_SIZE = 64
LEARNING_RATE = 0.01
EPOCHS = 20

5. 主要训练代码

w = np.zeros((train_datas.shape[1], ))  
# w 的 shape 为: (64, ), 一维数组, 只有一个维度, 并且该维度长度为64
b = 0
acc_list = []  # 存放测试集准确率, 方便后面绘图

for epoch in range(EPOCHS):
    cur = 0
    while cur < train_num:  # 训练使用了的数据长度小于训练数据总长度
        # 取出当前的训练数据
        current_data = train_datas[cur: cur + BATCH_SIZE, :]  # shape : (64, 64)
        current_labels = train_labels[cur: cur + BATCH_SIZE] # shape: (64,)

        y_hat = np.matmul(current_data, w) + b  # np.matmul() 表示进行向量间的点乘

$$\hat{\mathbf{y}}=\mathbf{x}\cdot \mathbf{w}+b$$
其中 $\mathbf{x}$的形状: [64, 64], $\mathbf{w}$的形状[64,], 得到的结果形状为[64,]

		# 将得到的结果转换为对应标签
        y_hat[y_hat >= 0] = 1
        y_hat[y_hat < 0] = -1

$$\mathrm{sign}(x)=\{\begin{array}{ll}& +1,x⩾0\\ & -1,x<0\end{array}$$

        # 得到分类错误的数据索的引矩阵
        flags = y_hat != current_labels
        # flags 的形状为: (64,)
        
        w += np.mean(current_labels[flags].reshape((-1,1)) * current_data[flags], 0)
        b += np.mean(current_labels[flags])

根据更新策略有:
$$\begin{gathered} w\leftarrow w+\eta y_i{x}_i \\ b\leftarrow b+\eta y_i \end{gathered}$$
假设此次分类错误的数据有38个, 则:

• current_labels[flags]的形状为: [38,], 经过reshape((-1,1))后的形状为: [38, 1]
• current_data[flags]的形状为: [38, 64]

w进行更新时:
两者进行元素级别的乘法运算时, 会将current_labels[flags]广播为[38, 64]
$$current\_labels[flags]=\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ ...\\ y_{38}\end{array}\right]\to \left[\begin{array}{cccc}{y}_1^1& y_1^2& ...& y_1^{64}\\ y_2^1& y_2^2& ...& y_2^{64}\\ y_3^1& y_3^2& ...& y_3^{64}\\ ...& ...& ...& ...\\ y_{38}^1& y_{38}^2& ...& y_{38}^{64}\end{array}\right]$$
即将第一列复制64次

最后进行元素级别的乘法运算 (作用是对每个样本的输入向量的每个特征进行加权调整，方向由标签决定) 得到形状为[38, 64]的矩阵
最后对第0个维度求均值, 得到形状为[64,]的矩阵(消除第0个维度)

        cur += BATCH_SIZE  # 对下一批次数据进行计算

    acc = evaluate(w, b, test_datas, test_labels)  # 对测试集进行 acc 计算
    print('Epoch:%d, accuracy:%.4f'%(epoch+1,acc))
    acc_list.append(acc)
"""
Epoch:1, accuracy:0.6889
Epoch:2, accuracy:0.7083
Epoch:3, accuracy:0.7194
Epoch:4, accuracy:0.7694
Epoch:5, accuracy:0.8028
Epoch:6, accuracy:0.7528
Epoch:7, accuracy:0.8389
Epoch:8, accuracy:0.8500
Epoch:9, accuracy:0.8611
Epoch:10, accuracy:0.8722
Epoch:11, accuracy:0.8722
Epoch:12, accuracy:0.8833
Epoch:13, accuracy:0.8778
Epoch:14, accuracy:0.8750
Epoch:15, accuracy:0.8750
Epoch:16, accuracy:0.8667
Epoch:17, accuracy:0.8722
Epoch:18, accuracy:0.8806
Epoch:19, accuracy:0.8833
Epoch:20, accuracy:0.8722

"""

使用sklearn实现

from sklearn.linear_model import Perceptron

clf = Perceptron()
clf.fit(train_datas, train_labels)

acc = clf.score(test_datas, test_labels)

print("acc: ", acc)
"""
输出;
acc:  0.8666666666666667
"""

6. 一些函数

# 计算 acc
def evaluate(w, b, datas, labels):
    y_hat = np.matmul(datas, w) + b
    y_pred = (y_hat>= 0).astype(int)
    y_pred[y_pred==0] = -1
    acc = np.mean(y_pred == labels)
    
    return acc

# 绘制 acc 曲线
def display_data(x, y, xlabel, y_label, title=None):
    plt.plot(x, y)
    # 添加网格信息
    plt.grid(True, linestyle='--', alpha=0.5) #默认是True，风格设置为虚线，alpha为透明度
    # 添加坐标轴标签
    plt.xlabel(xlabel)
    plt.ylabel(y_label)
    plt.title(title)
    plt.show()

x = range(1, len(acc_list)+1)
display_data(x, acc_list, 'epoch', 'acc')

输出acc曲线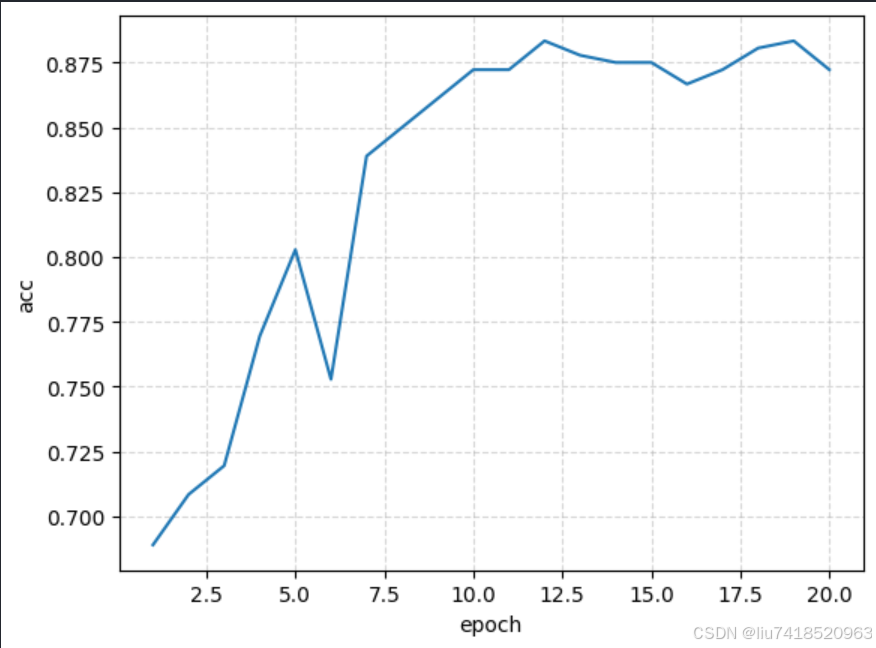

7. 结语

• 这篇文章大部分是一位大佬的代码,我只是对其进行了解释和添加了注释, 但是已经找不到原作者了, 如果有同学发现请告诉我
• 感知机是用于线性可分的数据集, 但是这篇文章的数据集明显是线性不可分的, 故仅仅用于学习基本流程
• 如有错误, 请狠狠的告诉我! 谢谢观看