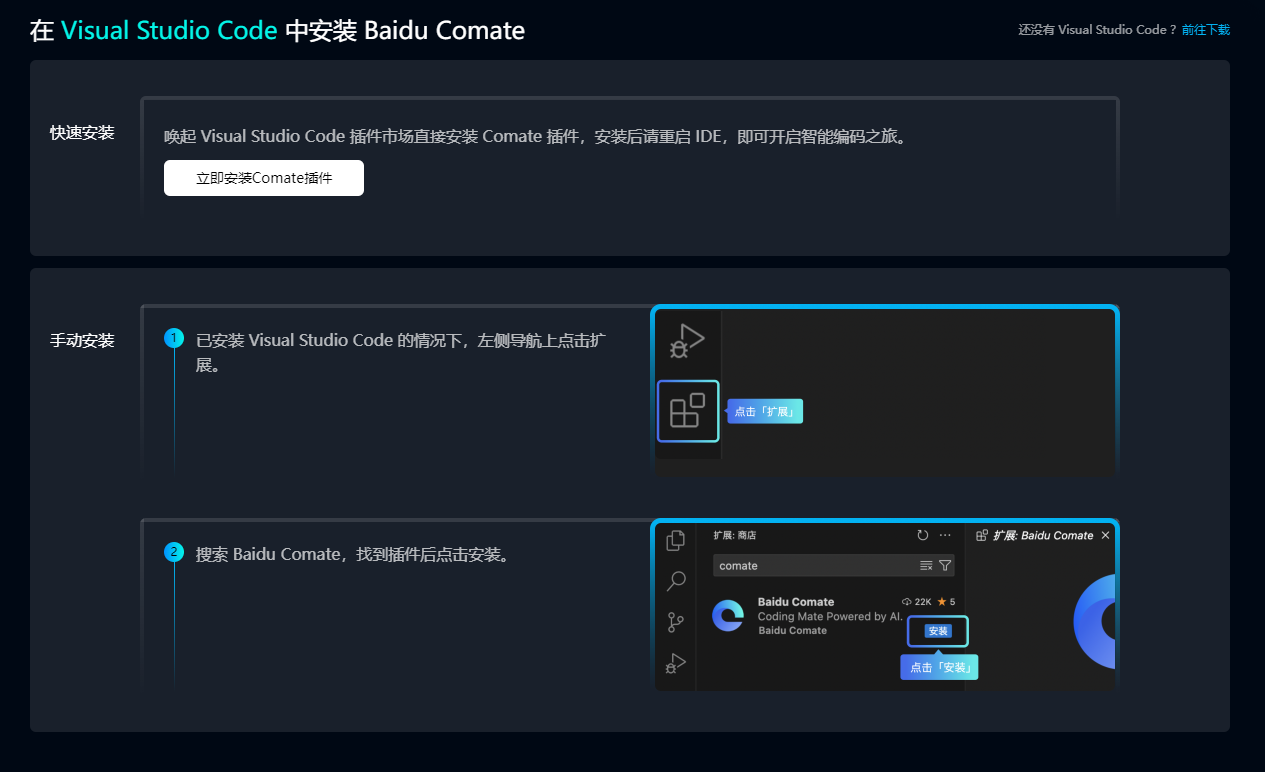
C. Another Array Problem(Codeforces Round #840 (Div. 2) and Enigma 2022 - Cybros LNMIIT)
对mx左边的数,选在mx左边的区间[1,id-1](长度最少是2),那么[1,id-1]里的数就换成了abs(a[1]-[id-1])三个数的总和,全换成a[1],全换成a[3],全换成abs(a[1]-a[2]),全换成abs(a[2]-a[3])=j),把从i~j的数全换成abs(a[i]-a[j])思路:当n>3的时候,我们可以把数组里的数全换成最大值mx,假设mx坐标为id。再对[1,id
You are given an array aa of nn integers. You are allowed to perform the following operation on it as many times as you want (0 or more times):
- Choose 22 indices ii,jj where 1≤i<j≤n1≤i<j≤n and replace akak for all i≤k≤ji≤k≤j with |ai−aj||ai−aj|
Print the maximum sum of all the elements of the final array that you can obtain in such a way.
Input
The first line contains a single integer tt (1≤t≤1051≤t≤105) — the number of test cases.
The first line of each test case contains a single integer nn (2≤n≤2⋅1052≤n≤2⋅105) — the length of the array aa.
The second line of each test case contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤1091≤ai≤109) — the elements of array aa.
It's guaranteed that the sum of nn over all test cases does not exceed 2⋅1052⋅105.
Output
For each test case, print the sum of the final array.
Example
input
Copy
3
3
1 1 1
2
9 1
3
4 9 5
output
Copy
3 16 18
题意:给一个长度为n的数组a,
任选两个坐标i,j(i!=j),把从i~j的数全换成abs(a[i]-a[j])
求最大元素和
思路:当n>3的时候,我们可以把数组里的数全换成最大值mx,假设mx坐标为id
对mx左边的数,选在mx左边的区间[1,id-1](长度最少是2),那么[1,id-1]里的数就换成了abs(a[1]-[id-1])
再对[1,id-1]操作一次,那么[1,id-1]里的数就变成了0
再对[1,id]操作一次,那么[1,id]都变成了mx
对mx右边的区间同理
那么当n==3的时候需要单独考虑,因为最大值可能是在下标为2的位置
那么所有情况就是
三个数的总和,全换成a[1],全换成a[3],全换成abs(a[1]-a[2]),全换成abs(a[2]-a[3])
取max就行了
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
typedef long long ll;
int n;
int a[N];
void sove(){
cin>>n;
ll mx=0;
for(int i=1;i<=n;i++){
cin>>a[i];
mx=max(mx,a[i]);
}
if(n>3){
cout<<n*mx<<endl;
return ;
}
if(n==1)cout<<a[1]<<endl;
else if(n==2){
cout<<max(a[1]+a[2],2*abs(a[1]-a[2]))<<endl;
}else{
ll ans=a[1]+a[2]+a[3];
ans=max(ans,a[1]*3);
ans=max(ans,a[3]*3);
ans=max(ans,abs(a[1]-a[2])*3);
ans=max(ans,abs(a[2]-a[3])*3);
cout<<ans<<endl;
}
}
signed main(){
int t;
cin>>t;
while(t--){
sove();
}
return 0;
}更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)