深度学习(6)TensorFlow基础操作二: 创建Tensor
深度学习(6)TensorFlow基础操作二: 创建Tensor一. 创建方式1. From Numpy,List2. zeros,ones(1) tf.zeros()(2) tf.zeros_like()(3) tf.ones()与tf.ones_like()3. Fill4. Normal(正态分布)6. Random Permutation(随机打散)二. 典型应用1. Scalar标量在神
深度学习(6)TensorFlow基础操作二: 创建Tensor
一. 创建方式
- from numpy,list
由numpy或者list类型的数据转换; - zeros,ones
创建全是0或者全是1的Tensor; - fill
创建填满任意数字的Tensor; - random
随机化初始Tensor; - constant
用constant来创建Tensor;
1. From Numpy,List
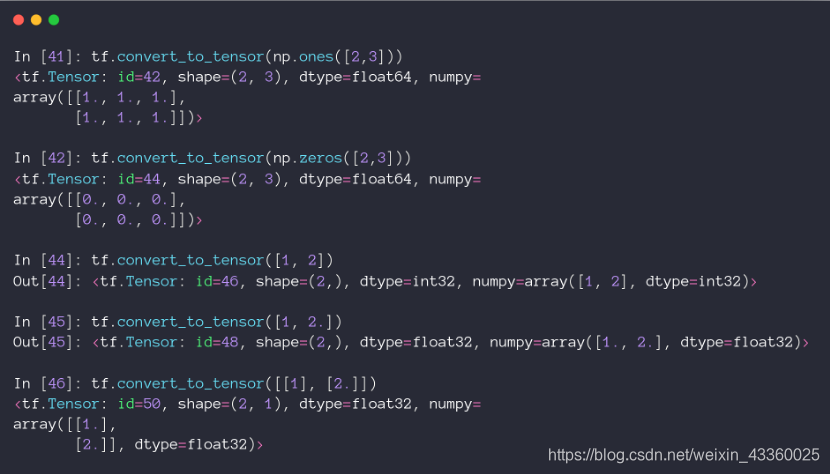
- 直接使用
tf.convert_to_tensor()函数即可完成由Numpy或者List类型到Tensor类型的转换;
2. zeros,ones
(1) tf.zeros()
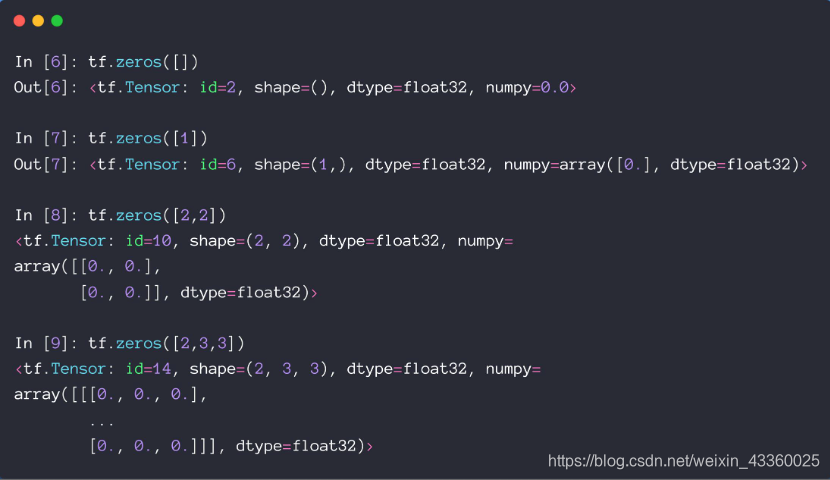
tf.zeros()中的参数是shape;tf.zeros([]): 新建一个标量(Saclar)其中元素为0的Tensor;tf.zeros([1]): 新建一个向量(Vector)其中元素为0的Tensor;tf.zeros([2, 2]): 新建一个矩阵(Matrix)其中元素为0的Tensor; 其中[2, 2]代表新建的Tensor维度是2行2列;
(2) tf.zeros_like()
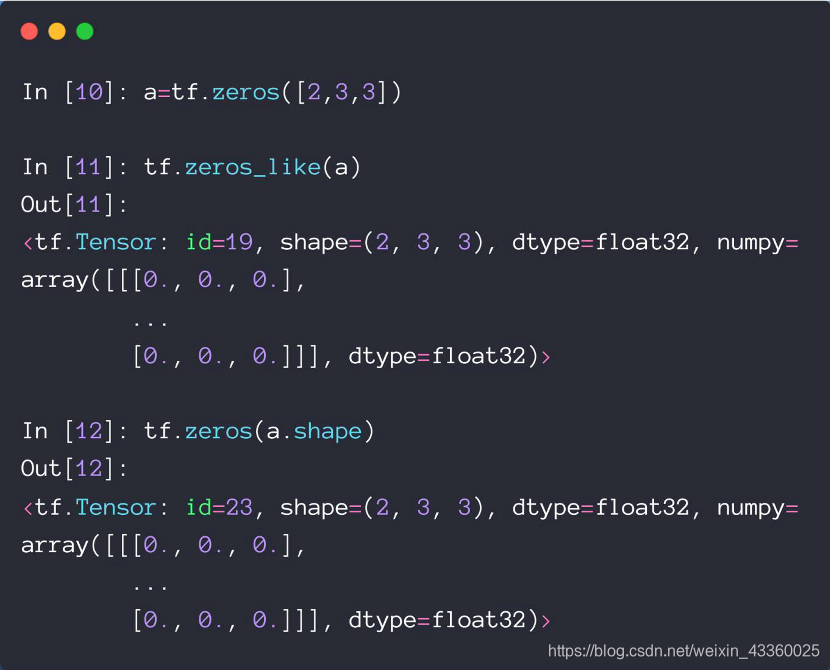
tf.zeros_like(a)相当于新建了一个和a维度相同的元素全为0的Tensor; 其作用与tf.zeros(a.shape)是完全一样的,使用哪个都可以;
(3) tf.ones()与tf.ones_like()
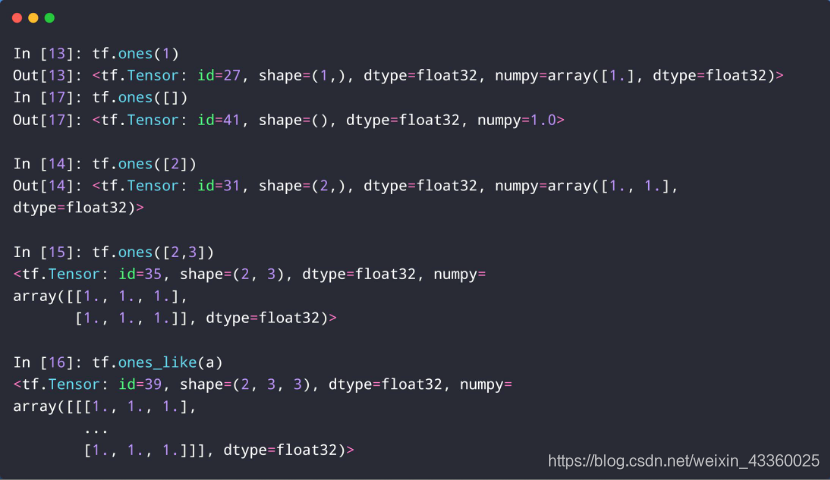
tf.ones和tf.ones_like的用法与tf.zeros和tf.zeros_like的用法是一样的,只不过里边的元素全为1;- zeros和ones方法最常见用于 y = w ∗ x + b y=w*x+b y=w∗x+b的参数 w w w和 b b b的初始化上;
3. Fill
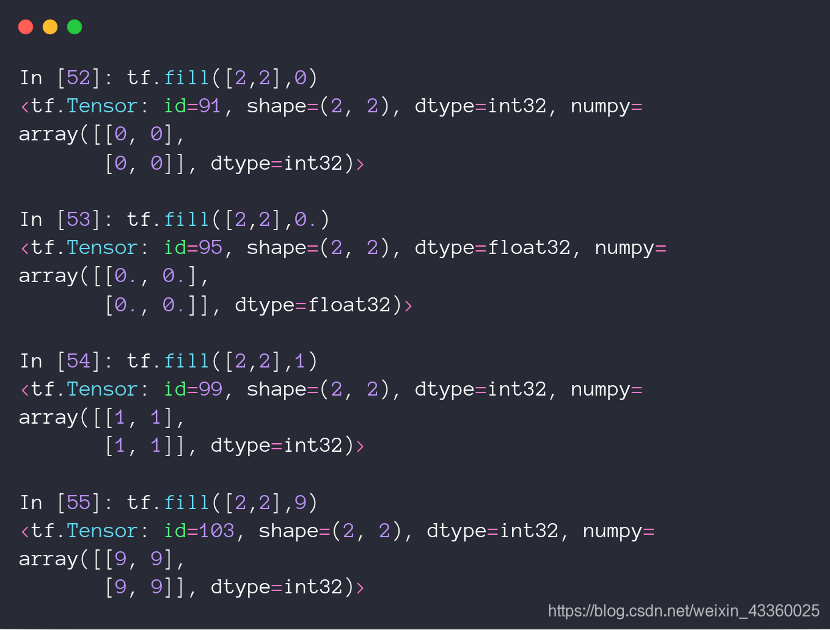
tf.fill([2, 2], 9)表示创建一个2行2列的Tensor,其中的元素都为9;
4. Normal(正态分布)
初始化参数的时候,不一定非要初始化成0或者1,有些时候将参数初始化成均匀分布或者正态分布,其模型的性能效果会更好。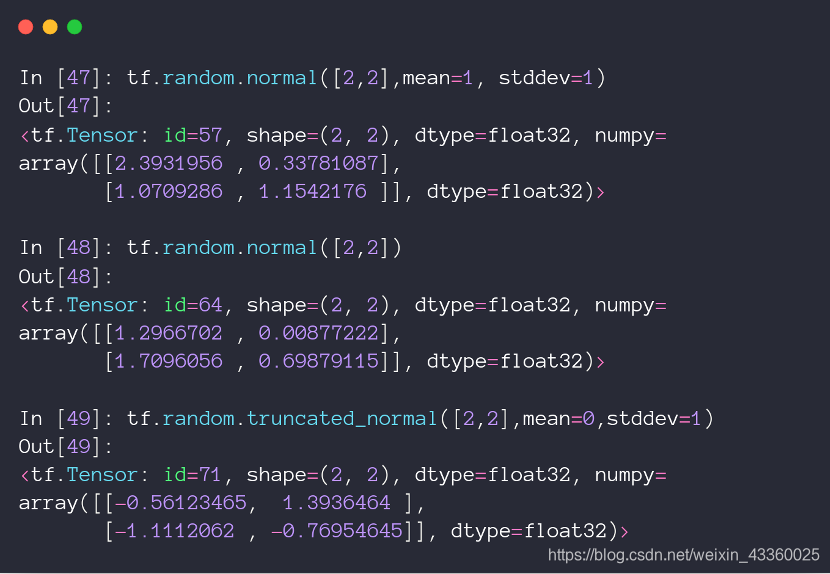
tf.random.normal([2, 2], mean=1, stddev=1)表示创建一个维度为[2, 2]的Tensor,其中mean=1代表均值为1,stddev=1代表方差为1,是一个标准的[1, 1]正态分布,即N(1,1);truncated_normal([2, 2], mean=0, stddev=1)表示截断的正态分布,就是在原来的[0,1]正态分布上截去了某一部分元素,例如: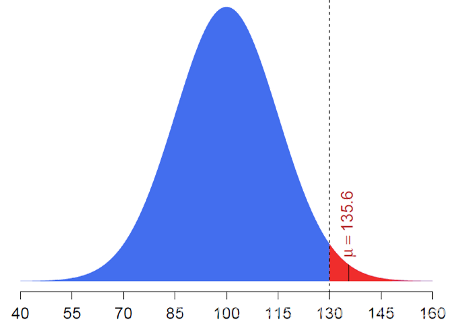
将 μ > 130 μ>130 μ>130的值截去,这样做的好处在于,Sigmoid函数会在大于某值(例如130)或者小于某值的时候,梯度接近于0,这样就会出现Gradient Vanish,即梯度消失问题,这时参数的更新就会变得非常困难,为了避免这种现象,就会使用truncated_normal(),这样会比normal()直接初始化好一些;
5. Uniform(均匀分布)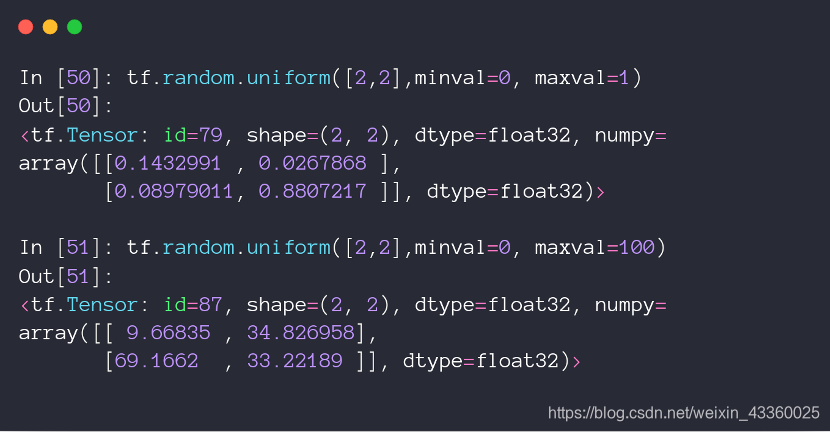
tf.random.uniform([2, 2], minval=0, maxval=1)表示数据从在服从(0, 1)的均匀分布中进行采样而来;tf.random.uniform([2, 2], minval=0, maxval=100)表示数据从在服从(0, 100)的均匀分布中进行采样而来;
6. Random Permutation(随机打散)
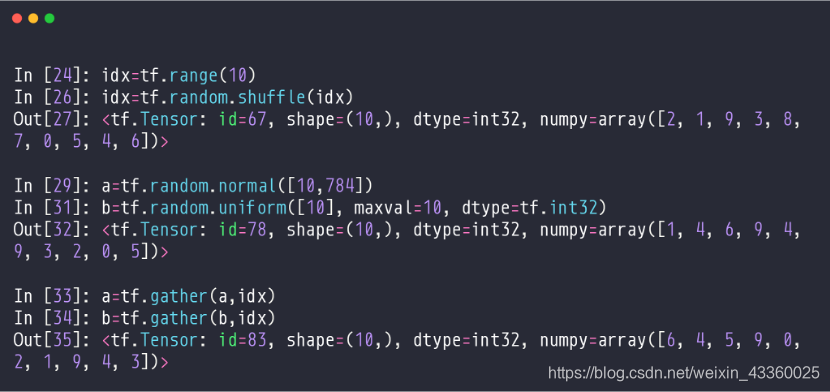
(1) 设一组图片的维度为 [ 64 , 28 , 28 , 3 ] [64, 28, 28, 3] [64,28,28,3],其中64为batch,有些时候我们需要将这64张图片顺序打乱,即打散操作。首先我们需要将这64张图片加上0~63的索引,再将索引打散;
(2) idx = tf.random.shuffle(isx): 将新建的 [ 0 , 9 ] [0, 9] [0,9]的idx(即索引)进行打散操作,打散的结果为numpy = array([2, 1, 9, 3, 8, 7, 0, 5, 4, 6]);
(3) 用打散的索引结构去在a = tf.random.normal([10, 784])和b = tf.random.uniform([10], maxval=10, dtype=tf.int32)中取数据;
(4) a = tf.gather(a, idx): 在a中按照idx的结构取数据;
7. tf.constant
(1) tf.constant(1)表示创建一个值为 1 1 1的标量;
(2) tf.constant([1])表示创建一个值为 [ 1 ] [1] [1]的向量;
(3) tf.constant([1, 2.])表示创建一个值为 [ 1 , 2. ] [1, 2.] [1,2.]的标量;
(4) 使用tf.constant创建Tensor时,里边元素的维度必须一样,否则就会出错;
二. 典型应用
Typical Dim Data
- []
- [d]
- [h, w]
- [b, len, vec]
- [b, h, w, c]
- [t, b, h, w, c]
- …
1. Scalar标量在神经网络中的呈现方式([])
- [ ] [] []其实就是Scalar,即标量,如 0 0 0, 1. 1. 1., 2.2 2.2 2.2, … … …;
- 常用在 l o s s loss loss函数中, l o s s = M S E ( o u t , y ) loss = MSE(out,y) loss=MSE(out,y),其中 l o s s loss loss就是一个标量;
- accuracy(精度),为一个具体的数值,也是标量;
- l o s s loss loss具体计算的例子:
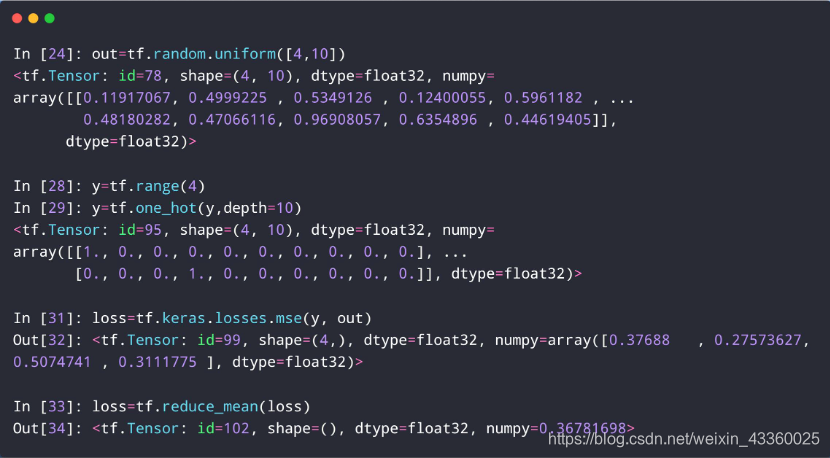
(1) out = tf.random.uniform([4, 10]): 使用随机均匀分布生成4张照片,照片共分为10类,也就是每张照片有10个维度;
(2) y = tf.range(4): 生成 l a b e l = [ 0 , 1 , 2 , 3 ] label = [0, 1, 2, 3] label=[0,1,2,3],也就是说我们假定第一张图片的label为0,第二张图片的label为1,第三张图片的label为2,第四张图片的label为3;
(3) y = tf.one_hot(y, depth=10): 使用one-hot编码方式进行编码,即:
0 : [ 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ] 0: [1., 0., 0., 0., 0., 0., 0., 0., 0., 0.] 0:[1.,0.,0.,0.,0.,0.,0.,0.,0.,0.]
1 : [ 0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ] 1: [0., 1., 0., 0., 0., 0., 0., 0., 0., 0.] 1:[0.,1.,0.,0.,0.,0.,0.,0.,0.,0.]
2 : [ 0. , 0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ] 2: [0., 0., 1., 0., 0., 0., 0., 0., 0., 0.] 2:[0.,0.,1.,0.,0.,0.,0.,0.,0.,0.]
3 : [ 0. , 0. , 0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. ] 3: [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.] 3:[0.,0.,0.,1.,0.,0.,0.,0.,0.,0.]
(4) loss = tf.kares.losses.mse(y, out): 使用kares.losses.mse()方法计算总损失值,即:
l o s s = ∑ ( y − o u t ) 2 loss=\sum{(y-out)^2} loss=∑(y−out)2
(5) loss = tf.reduce_mean(loss): 使用reduce_mean()方法计算平均损失值,即:
l o s s = 1 n ∑ ( y − o u t ) 2 loss=\frac{1}{n}\sum{(y-out)^2} loss=n1∑(y−out)2
可以看到最后的平均损失值 l o s s loss loss的shape = (),也就证明了 l o s s loss loss为一个标量。
2. Vector在神经网络中的呈现方式
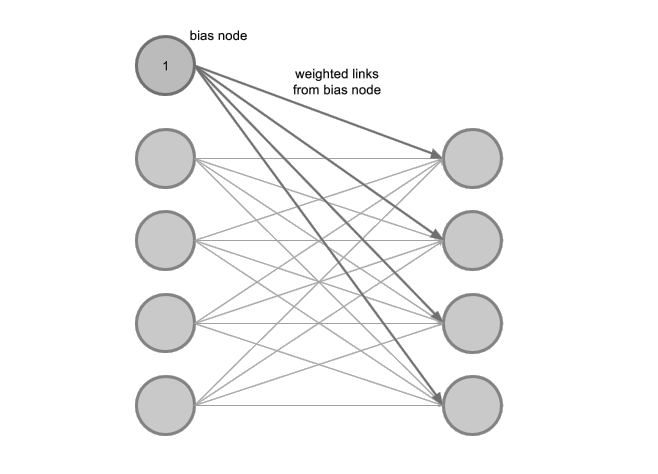
- Bias(偏置项)
- [out_dim]
在计算 Y = X @ W + b Y=X@W+b Y=X@W+b的时候, b b b就是偏置项Bias,他就是一个Vector,例如输出 o u t out out为0~9时,那么b的就是 [ 1 , 10 ] [1, 10] [1,10];
以 Y = X @ W + b Y=X@W+b Y=X@W+b升维为例: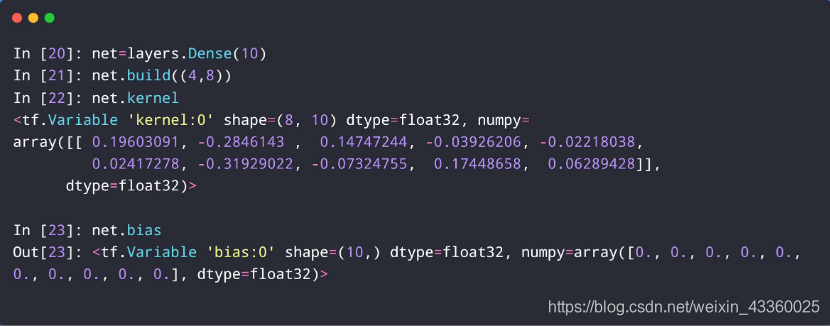
- [out_dim]
(1) layers.Dense()函数的功能是变化维度;
(2) net = layers.Dense(10): 将8维升到10维;
(3) net.kernel: 这里可以看出 w w w的shape = (8, 10);
(4) net.bias: 这里可以看出b的shape = (10,),还可以看出初始化默认值全部为0,即 [ 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ] [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.] [0.,0.,0.,0.,0.,0.,0.,0.,0.,0.];
3. Matrix在神经网络中的呈现方式
- input x: [b, vec_dim]
- weight: [input_dim, output_dim]
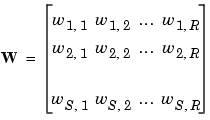

(1) x = tf.random.normal([4, 784]): 有4张照片,每张照片是 28 × 28 28×28 28×28,也就是784维;
(2) net = layers.Dense(10): 定义一个将图片维度变为10维的网络;
(3) net(x).shape: 将x放入到定义好的网络net中并查看shape;
(4) 可以看到net(x).shape为 [ 4 , 10 ] [4, 10] [4,10],即一个4行10列的矩阵;
(5) net.kernel.shape: 查看w的维度,为 [ 784 , 10 ] [784, 10] [784,10],即一个784行10列的矩阵, w w w的dim为2;
(6) net.bias.shape: 查看 b b b的维度,为 [ 10 ] [10] [10], b b b的dim为1;
4. Dim=3 Tensor
- x: [b, seq_len, word_dim]
- [b, 5, 5]
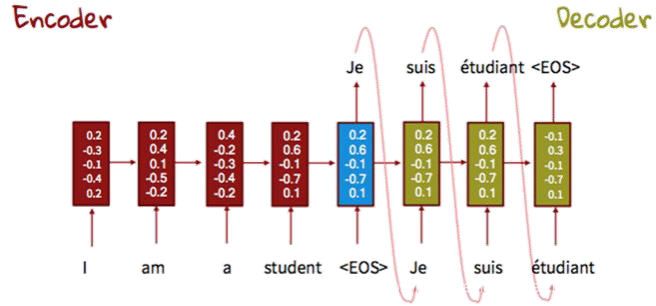
- [b, 5, 5]
例如: 每个句子有80个单词,每个单词有5个维度,那么一个句子的shape就为[1, 80, 5],如果有b个句子,那么这b个句子的shape就为[b, 80, 5];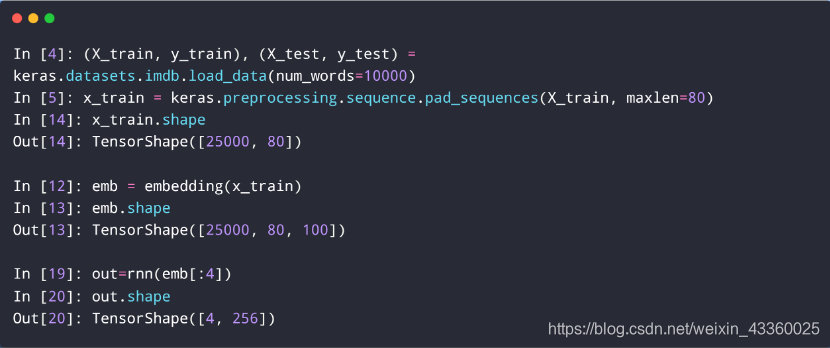
imdb是一个数据库,TensorShape([25000, 80])表示共有25000条影评,每条评价有80个单词,每个单词有100个维度,所以TensorShape为 [ 25000 , 80 , 100 ] [25000, 80, 100] [25000,80,100];
5. Dim=4 Tensor
- Image: [ b , h , w , 3 ] [b, h, w, 3] [b,h,w,3]
- feature maps: [ b , h , w , c ] [b, h, w, c] [b,h,w,c],其中b为一批图片的数目(即batch),h为图片的高(即height),w为图片的宽(即width),c为图片的通道数(即channel);

例如: 一张彩色图片高为h,宽为w,那么这张图片的shape就为 [ 1 , h , w , 3 ] [1, h, w, 3] [1,h,w,3]; 如果有b张图片的话,那么这b张图片的shape就为 [ b , h , w , 3 ] [b, h, w, 3] [b,h,w,3];
(1) tf.random.normal((4, 32, 32, 3)): 4张32×32的彩色图片;
(2) Conv2D: 卷积神经网络; channel由原来的3变为了16;
6. Dim=5 Tensor
- Single task: [ b , h , w , 3 ] [b, h, w, 3] [b,h,w,3]
- meta-learning:
- [ t a s k _ b , b , h , w , 3 ] [task\_b, b, h, w, 3] [task_b,b,h,w,3]
一个任务的shape为 [ b , h , w , 3 ] [b, h, w, 3] [b,h,w,3],那么有多个任务的时候,shape就为 [ t a s k _ b , b , h , w , 3 ] [task\_b, b, h, w, 3] [task_b,b,h,w,3];
- [ t a s k _ b , b , h , w , 3 ] [task\_b, b, h, w, 3] [task_b,b,h,w,3]
参考文献:
[1] 龙良曲:《深度学习与TensorFlow2入门实战》
[2]https://assessingpsyche.wordpress.com/2014/06/04/using-the-truncated-normal-distribution/
[3] https://blog.csdn.net/dcrmg/article/details/79797826
[4] https://medium.com/syncedreview/representations-for-language-from-word-embeddings-to-sentence-meanings-3fae81b2379a
[5] https://docs.gimp.org/2.4/en/gimp-images-in.html
[6] https://www.coursera.org/learn/learning-how-to-learn
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)