【机器学习】正则化对过拟合和欠拟合的影响
接下来我们总结若干应对各种问题的方法:修正过拟合(高方差):增加训练及数量、使用更少的特征、增加正则化参数的值修正欠拟合(高偏差):增加额外的特征、增加假设函数的复杂度和次方数、减小正则化参数的值。
模型过拟合和欠拟合的图像特征
偏差大表示欠拟合,而方差大表示过拟合,我们这一节再深入探讨下过拟合和欠拟合问题。一个经典的图如下: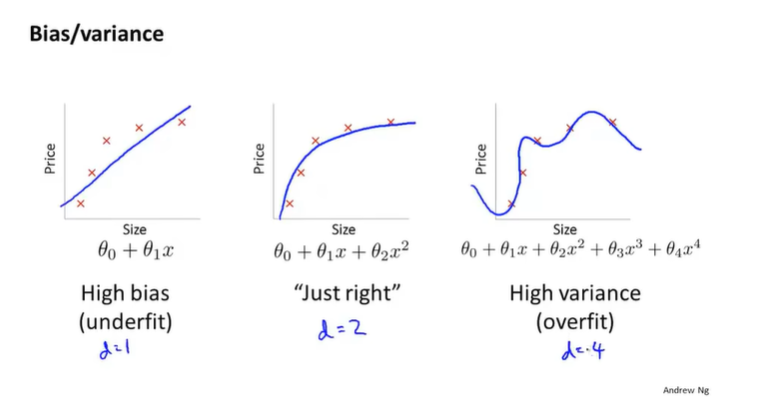
其中d=1为欠拟合,d=4为过拟合,而d=2则刚刚好。回顾下刚刚说的使用训练集和交叉验证集计算出来的误差(又称代价函数)Jtrain(θ)J_{train}(\theta)Jtrain(θ)和Jcv(θ)J_{cv}(\theta)Jcv(θ),当d=1的时候,模型欠拟合,那么Jtrain(θ)J_{train}(\theta)Jtrain(θ)和Jcv(θ)J_{cv}(\theta)Jcv(θ)都很大,因为模型对训练集的拟合都不好,对交叉验证集训练出来的结果只会更烂,此时一般来说Jtrain(θ)J_{train}(\theta)Jtrain(θ)和Jcv(θ)J_{cv}(\theta)Jcv(θ)很接近,但是Jcv(θ)J_{cv}(\theta)Jcv(θ)略高。当d=4的时候,模型过拟合,模型对训练集的拟合已经很好了,但是泛化能力很差,因此Jtrain(θ)J_{train}(\theta)Jtrain(θ)比较小,但是Jcv(θ)J_{cv}(\theta)Jcv(θ)比较大。Jtrain(θ)J_{train}(\theta)Jtrain(θ)和Jcv(θ)J_{cv}(\theta)Jcv(θ)图像如下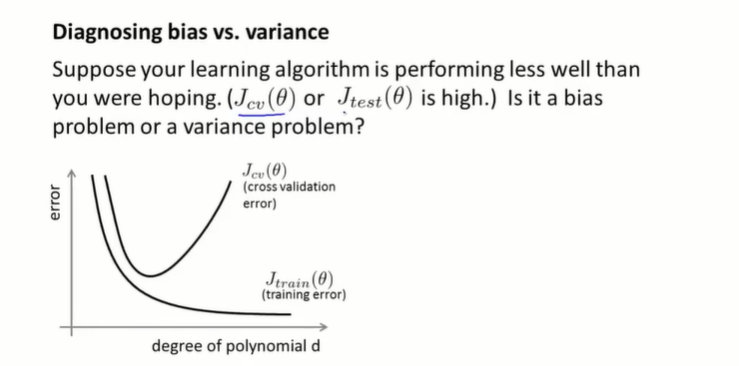
方差、偏差和正则化
本节继续深入讨论方差和偏差的关系,以及正则化是如何影响这两者的。
假设对于假设函数h(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4h(x)=\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\theta_4x^4h(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4我们使用如下的正则化代价函数训练J(θ)=12m∑i=1m(hθ(x(i))−y(i))2+λ2m∑j=1mθj2J(\theta) = \frac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})^2+\frac{\lambda}{2m}\sum_{j=1}^m\theta_j^2J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+2mλj=1∑mθj2那么可能会有如下图三种情况
左边是λ\lambdaλ非常大的情况,也就是对于任意偏差的惩罚都十分重,这时候图像会倾向于欠拟合(高偏差);右边是λ\lambdaλ非常小的情况,也就是对于任意偏差的惩罚都十分轻微,这时候图像会倾向于过拟合(高方差),就和没使用正则化差不多。只有正则化参数大小适中才能获得泛化能力强偏差小的模型。 另外我们设训练函数为Jtrain(θ)=12m∑i=1m(hθ(x(i))−y(i))2J_{train}(\theta) = \frac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})^2Jtrain(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
也就是去掉正则化项,同样,我们将交叉验证的代价函数和测试集的代价函数设置为Jcv(θ)=12mcv∑i=1mcv(hθ(xcv(i))−ycv(i))2J_{cv}(\theta) = \frac{1}{2m_{cv}}\sum_{i=1}^{m_{cv}} (h_\theta(x^{(i)}_{cv})-y^{(i)}_{cv})^2Jcv(θ)=2mcv1i=1∑mcv(hθ(xcv(i))−ycv(i))2Jtest(θ)=12mtest∑i=1mtest(hθ(xtest(i))−ytest(i))2J_{test}(\theta) = \frac{1}{2m_{test}}\sum_{i=1}^{m_{test}} (h_\theta(x^{(i)}_{test})-y^{(i)}_{test})^2Jtest(θ)=2mtest1i=1∑mtest(hθ(xtest(i))−ytest(i))2
我们会以每次翻一番的速度更新λ\lambdaλ的值,并且得出代价函数J(θ)J(\theta)J(θ)最小的时候的θ\thetaθ值。然后通过计算出的θ\thetaθ计算Jcv(θ)J_{cv}(\theta)Jcv(θ),其基本计算过程如下:
try λ=0→minJ(θ)→θ(1)→Jcv(θ(1))try\:\lambda=0\to minJ(\theta)\to \theta^{(1)}\to J_{cv}(\theta^{(1)})tryλ=0→minJ(θ)→θ(1)→Jcv(θ(1))
try λ=0.01→minJ(θ)→θ(2)→Jcv(θ(2))try\:\lambda=0.01\to minJ(\theta)\to \theta^{(2)}\to J_{cv}(\theta^{(2)})tryλ=0.01→minJ(θ)→θ(2)→Jcv(θ(2))
try λ=0.02→minJ(θ)→θ(3)→Jcv(θ(3))try\:\lambda=0.02\to minJ(\theta)\to \theta^{(3)}\to J_{cv}(\theta^{(3)})tryλ=0.02→minJ(θ)→θ(3)→Jcv(θ(3))
try λ=0.04→minJ(θ)→θ(4)→Jcv(θ(4))try\:\lambda=0.04\to minJ(\theta)\to \theta^{(4)}\to J_{cv}(\theta^{(4)})tryλ=0.04→minJ(θ)→θ(4)→Jcv(θ(4))
…
try λ=10.24→minJ(θ)→θ(12)→Jcv(θ(12))try\:\lambda=10.24\to minJ(\theta)\to \theta^{(12)}\to J_{cv}(\theta^{(12)})tryλ=10.24→minJ(θ)→θ(12)→Jcv(θ(12))
假设我们计算出Jcv(θ(5))J_{cv}(\theta^{(5)})Jcv(θ(5))的值最小,那么我们可以用选择出来的θ(5)\theta^{(5)}θ(5)来计算出其Jtest(θ(5))J_{test}(\theta^{(5)})Jtest(θ(5))的值,该值可以衡量模型对新样例泛化的能力
之前我们谈到,如果正则化参数很小,那么会过拟合;反之则会欠拟合,我们画出正则化参数和Jcv(θ)J_{cv}(\theta)Jcv(θ)以及Jtrain(θ)J_{train}(\theta)Jtrain(θ)的关系。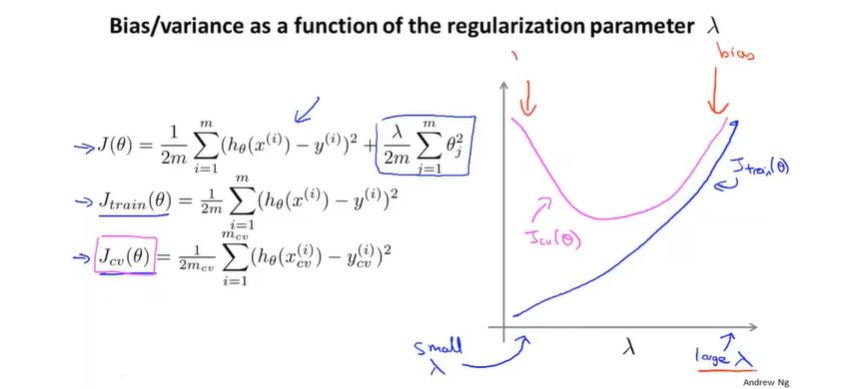
其中紫红色的为Jcv(θ)J_{cv}(\theta)Jcv(θ),蓝色的为Jtrain(θ)J_{train}(\theta)Jtrain(θ),因为λ\lambdaλ小的时候,过拟合对训练集拟合很好,但是泛化能力很差;而λ\lambdaλ过大的时候,欠拟合对训练集都拟合不充分,其泛化能力也很差
学习曲线
学习曲线可以验证你的模型是否正确,或者改进算法的精度。我们以训练集的数量m作为横轴,将代价函数作为纵轴,那么可以得出如下的图像: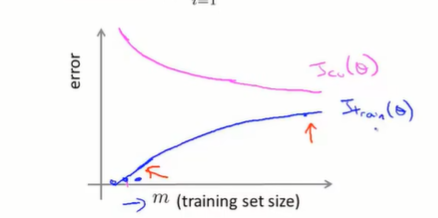
如果只有训练集一个样例,那么训练集可以拟合的十分精准——只需要找到任意一条经过该点的曲线便可,但是其泛化能力是很差的。随着样例数量增加,实际上假设函数无法精确经过每一个样例,此时Jtrain(θ)J_{train}(\theta)Jtrain(θ)会有所上升,但是逐渐总结出规律后,样例和假设函数的偏差不会太大,因此Jtrain(θ)J_{train}(\theta)Jtrain(θ)在上升后会逐渐趋于平缓。而模型的泛化能力则是随着训练集样本的增加而逐渐增强的,因此Jcv(θ)J_{cv}(\theta)Jcv(θ)一开始会很高,然后逐渐下降。
在欠拟合(高偏差)的情况下,如果我们增大训练量会怎么样?(如图右边)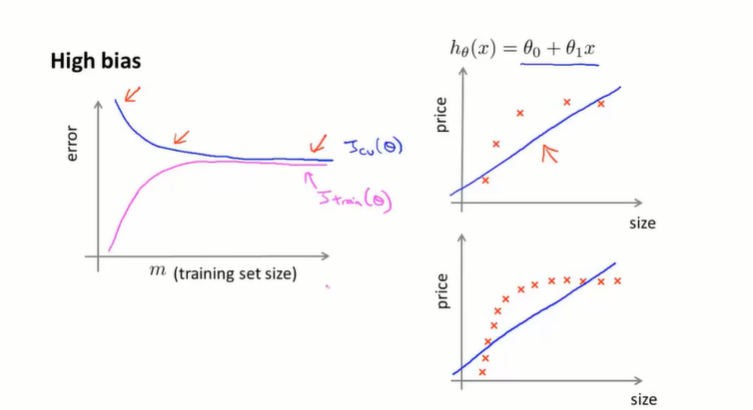
结果是没什么用,因为假设函数次数不够,哪怕增加了样例其假设函数(也就是误差)还是很高。同样的,连训练集都搞不定就更别提交叉验证集了,其结果是Jtrain(θ)J_{train}(\theta)Jtrain(θ)和Jcv(θ)J_{cv}(\theta)Jcv(θ)都很高。其结论是,如果在欠拟合的情况下,增大训练集数据量会使得Jtrain(θ)J_{train}(\theta)Jtrain(θ)和Jcv(θ)J_{cv}(\theta)Jcv(θ)逐渐趋于平缓,但其值依旧较高。
在过拟合(高方差)的时候,如果增加样本量会如何?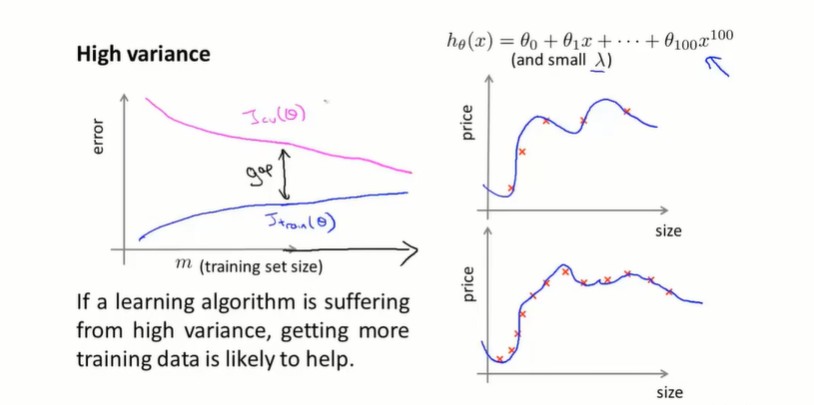
可以看出样本小的时候对训练集拟合很好,但是泛化能力很差。随着样本量增大,假设函数很难将所有训练集样本都拟合的很好,因此Jtrain(θ)J_{train}(\theta)Jtrain(θ)会轻微上升,但是换来的是其泛化能力的增强——因为模型学会应对更多情况了因此Jcv(θ)J_{cv}(\theta)Jcv(θ)会逐渐下降,而如果持续增大样本来给你,其Jcv(θ)J_{cv}(\theta)Jcv(θ)和Jtrain(θ)J_{train}(\theta)Jtrain(θ)会逐渐靠近,最后Jtrain(θ)J_{train}(\theta)Jtrain(θ)只比Jcv(θ)J_{cv}(\theta)Jcv(θ)大一些,而总的来说,两个值都会比在欠拟合情况下要小得多
总结
接下来我们总结若干应对各种问题的方法:
修正过拟合(高方差):增加训练及数量、使用更少的特征、增加正则化参数的值
修正欠拟合(高偏差):增加额外的特征、增加假设函数的复杂度和次方数、减小正则化参数的值
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)