回归和分类是机器学习的两大重要的任务。作为入门打的，相对比较简单的线性回归任务，实现方式有很多，可以采用手写（硬撸）方式，也可以采用现在流行的pytorch框架实现。

首先回顾一下线性回归的基本定义：回归任务简单来说就是为输入的一组因变量和自变量之间关系建模的一类方法。在很多领域，回归经常表示输入与输出之间的关系，同时线性则代表了自变量和因变量之间存在的是一种线性关系，不需要做非线性变换，即可实现拟合。其模型的表示可以用简洁的矩阵运算加以表示：

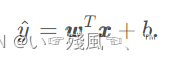
第一种方法：手动更新w和b

有关于线性回归的知识点，网上有很多教程，这里不再一一赘述，下面直接介绍两种方式的线性回归实现方法，第一种是人为更新参数的方式：

import numpy as np
import torch



# 设置随机数种子，使得每次运行代码生成的数据相同
np.random.seed(42)
# 生成随机数据
x = np.random.rand(100,1)  # 该函数括号内的参数指定的是返回结果的形状
y = 1 + 2*x + 0.1 * np.random.randn(100,1)  # 返回的结果是服从均值为0，方差为1的标准正态分布，而不是局限在0-1之间，也可以为负值
# 将数据转换为pytorch tensor 格式
x_tensor = torch.from_numpy(x).float()
y_tensor = torch.from_numpy(y).float()




# 设置超参数
# 学习率                    迭代次数
learning_rate = 0.1 
num_epochs = 1000



# 初始化参数
# 使用pytorch的randn函数初始化参数w和zeros函数初始化参数b
# 其中randn函数会生成一个均值为0，标准差为1的随机张量；而zeros函数会生成一个全部元素都是0的张量
# requires_grad 为 True表示希望在反向传播时计算梯度
w = torch.randn(1,requires_grad = True)
# w = torch.zeros(1,requires_grad = True)   
# 测试后发现结果一样
b = torch.zeros(1,requires_grad = True)



# 开始训练
for epoch in range(num_epochs):
    # 计算预测值
    y_pred = x_tensor * w +b
    #print('x是否为叶子结点:',x_tensor.is_leaf)
    # 计算损失
    loss = ((y_pred - y_tensor)**2).mean()
    
    # 反向传播
    loss.backward()
    
    # 更新参数
    # 被with torch.no_grad()包住的代码，不用跟踪反向梯度计算
    with torch.no_grad():
        w -= learning_rate * w.grad
        b -= learning_rate * b.grad
        #清空梯度
        w.grad.zero_()
        b.grad.zero_()    
    
# 输出训练后的参数
print('w:',w)
print('b:',b)



# 对于detach()方法的解释：实际上，detach()就是返回一个新的tensor，并且这个tensor是从当前的计算图中分离出来的。但是返回的tensor和原来的tensor是共享内存空间的。
# 数据可视
import matplotlib.pyplot as plt
# 绘制数据散点
plt.plot(x,y,'o')
# 绘制拟合的直线
plt.plot(x_tensor.numpy(),y_pred.detach().numpy())
plt.show()

这里最重要的是模型的训练部分：

# 开始训练

for epoch in range(num_epochs):
    # 计算预测值
    y_pred = x_tensor * w +b
    #print('x是否为叶子结点:',x_tensor.is_leaf)
    # 计算损失
    loss = ((y_pred - y_tensor)**2).mean()
    
    # 反向传播
    loss.backward()
    
    # 更新参数
    # 被with torch.no_grad()包住的代码，不用跟踪反向梯度计算
    with torch.no_grad():
        w -= learning_rate * w.grad
        b -= learning_rate * b.grad
        #清空梯度
        w.grad.zero_()
        b.grad.zero_()
    
    
# 输出训练后的参数
print('w:',w)
print('b:',b)

在每一次迭代过程中首先是计算损失，然后进行反向传播，在做完反向传播（此时已经对w和b进行偏导计算了）后更新w和b，同时清空这一轮计算的w和b的梯度结果。最后打印训练后的w和b的值，打印结果如下：

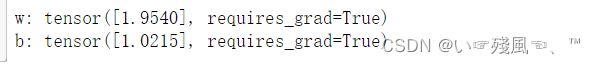
第二种方式：使用pytorch框架

 在使用pytroch框架后，与之前手动更新参数不同的是没有对w和b进行初始化，同时采用了优化器和损失函数算法。另外，模型训练方面也有所不同，采用的是 

 optimizer.step()

更新参数，详细代码如下所示：

import numpy as np
import torch
import torch.nn as nn


# 设置随机数种子，使得每次运行代码生成的数据相同
np.random.seed(42)


# 生成随机数据
x = np.random.rand(100,1)  #100行1列
y = 1 + 2 * x + 0.1 * np.random.randn(100,1
# 将数据转换为pytorch tensor
x_tensor = torch.from_numpy(x).float()
y_tensor = torch.from_numpy(y).float()



# 设置超参数
learning_rate  = 0.1
num_epochs = 500



# 定义输入数据的维度和输出数据的维度
input_dim  = 1
output_dim =  1
# 定义模型
model  = nn.Linear(input_dim,output_dim)  # 输入为一维，输出为一维的线性回归模型
# 定义损失函数和优化器
criterion = nn.MSELoss()   # 使用MSE损失函数计算
optimizer = torch.optim.SGD(model.parameters(),lr = learning_rate)


# 开始训练
for epoch in range(num_epochs):
    # 将输入数据投喂给模型
    y_pred  =  model(x_tensor)
    # 计算损失
    loss = criterion(y_pred,y_tensor)
    # 清空梯度
    optimizer.zero_grad()
    # 反向传播
    loss.backward()
    # 更新参数
    optimizer.step()
# 输出训练以后的参数w和b
print(f"w:{model.weight.data}")
print(f"b:{model.bias.data}")


# 数据可视化
import matplotlib.pyplot as plt
# 绘制数据散点
plt.plot(x,y,'o')
# 绘制拟合的直线
plt.plot(x_tensor.numpy(),y_pred.detach().numpy())
plt.show()