1.1 什么是机器学习

​ Machine learning algorithms:

​ -Supervised learning

​ -Unsupervised learning

​ (Reinforcement learning)

1.2 Supervised learning 监督学习

x(input) ------> y(output/label) (输入输出间的映射关系)

​ 给算法数据集(input)，数据集中有正确答案，通过数据集训练模型(model),最后让算法通过自动学习进而可以给出更多的正确答案(output)。

Regression(回归)
Classification(分类)

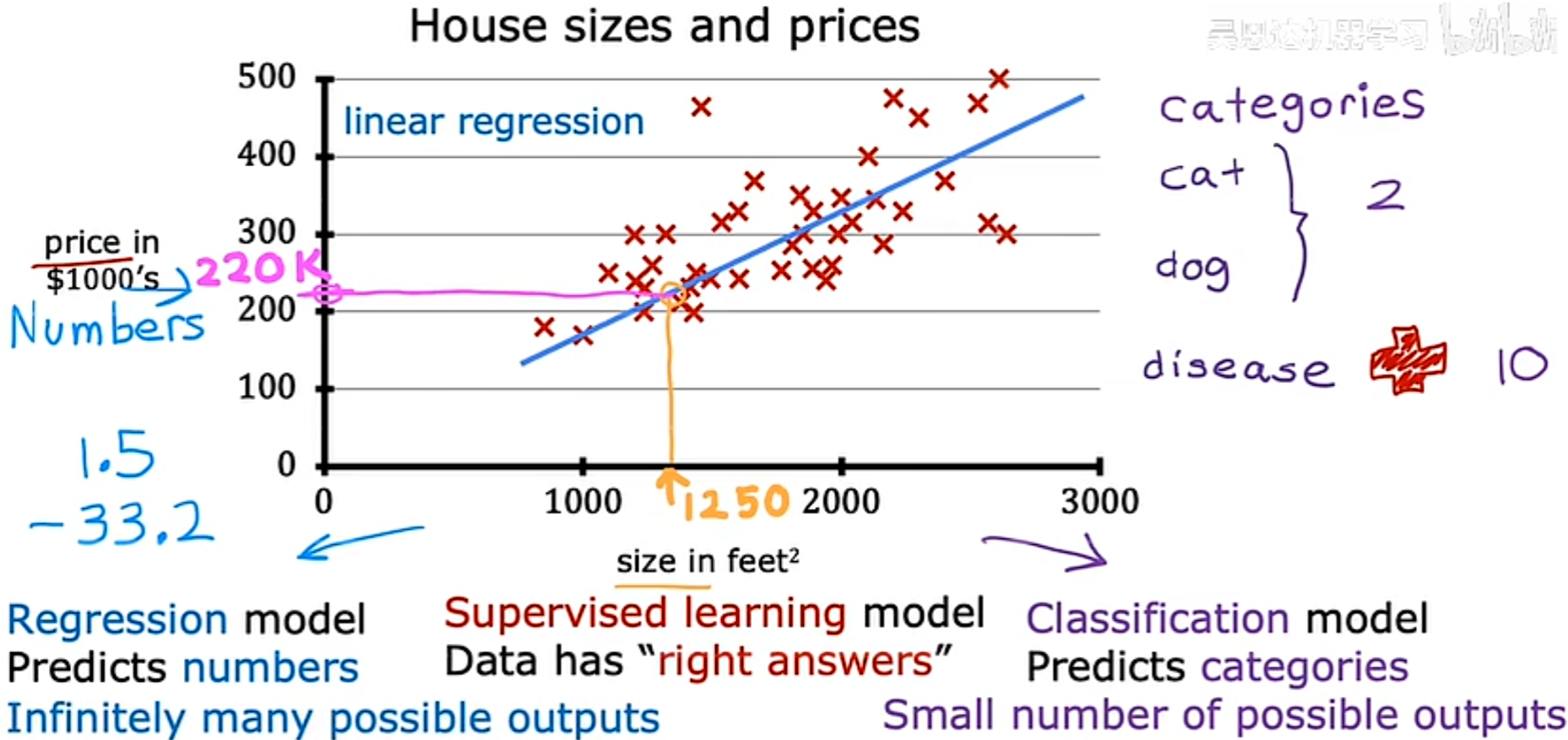
Regression(回归) Algorithm：

​ 从无数的可能中预测一种可能的结果输出。

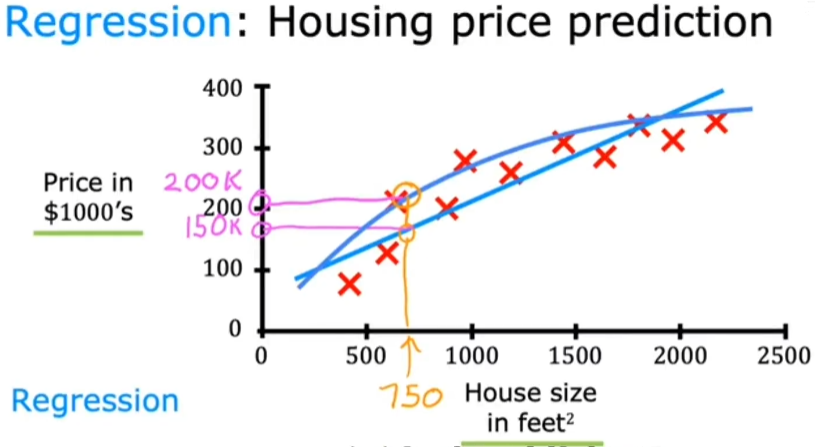
Classification(分类) Algorithm:

​ 与Regression(回归)不同的是，分类方法只试图预测一小部分可能的输出或类别。

eg：

​ 癌症预测，通过肿瘤的大小判断，输出要么为良性，要么为恶性。

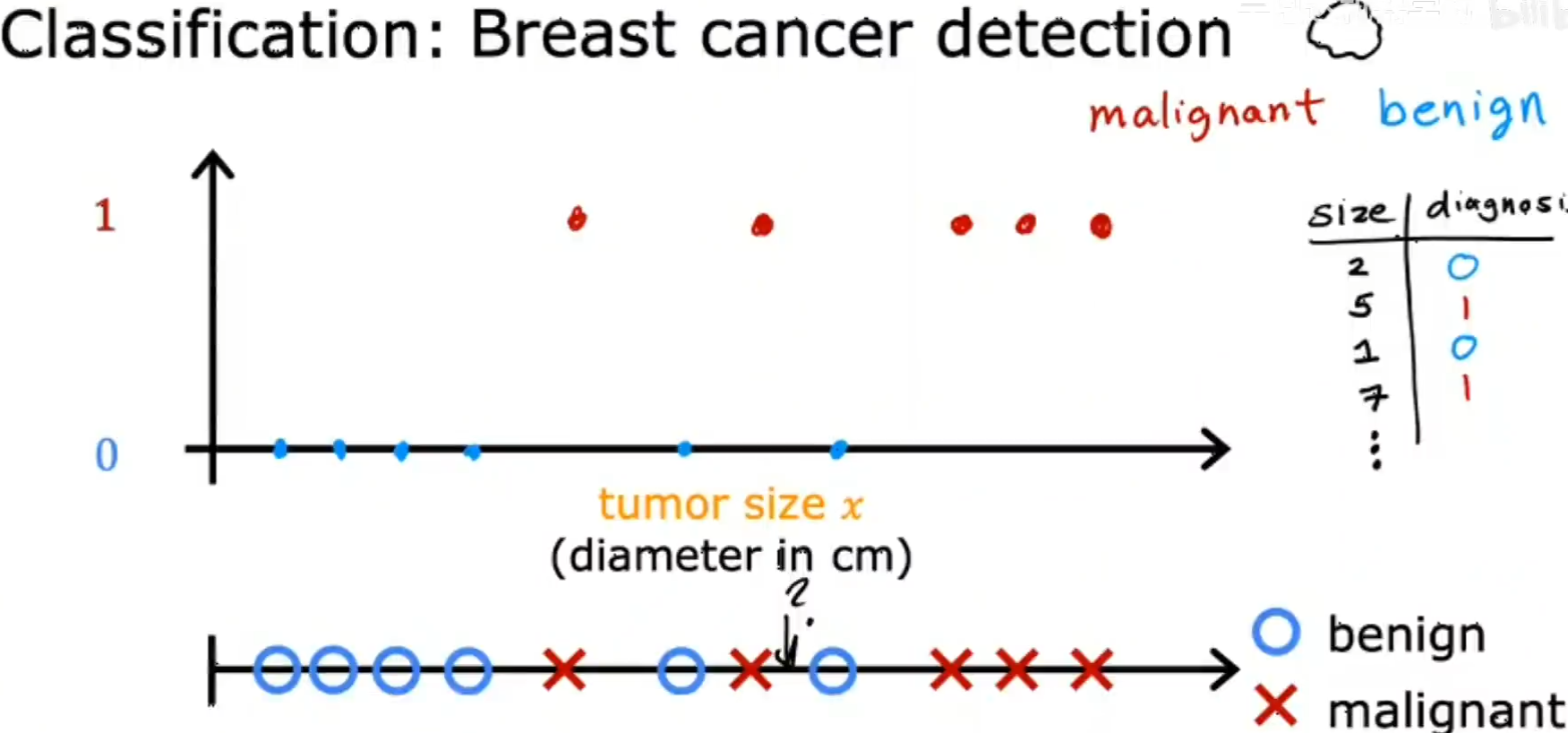
​ 当然也可能有多种可能性，例如也可以通过输入的图片，判断是狗或猫…

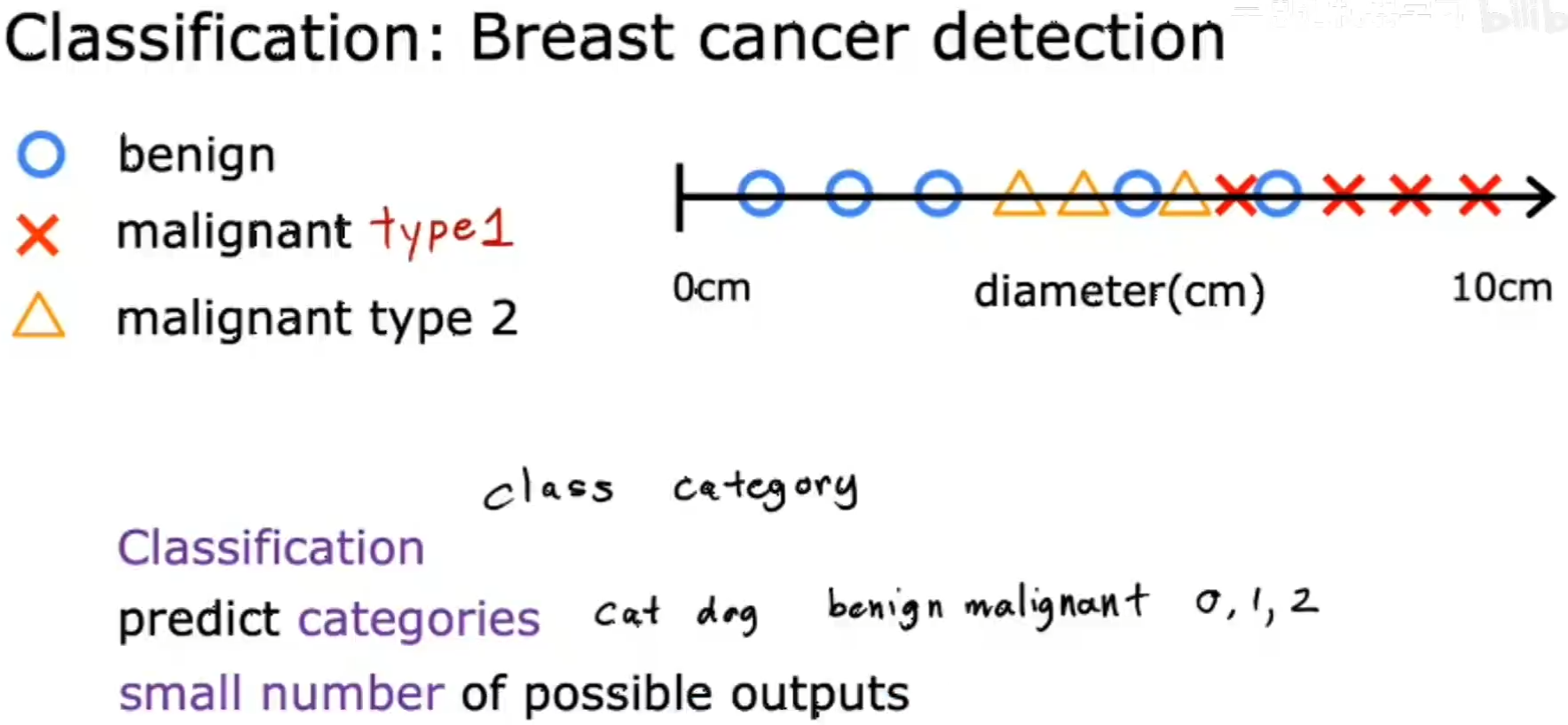
​ 有时候可能会不止一种特征，例如判断癌症阶段时，需要通过患者的年龄和肿瘤大小两个方面来进行判断，此时需要算法判断出一种边界值来区分癌症具体数据的某一个阶段(粉线)：

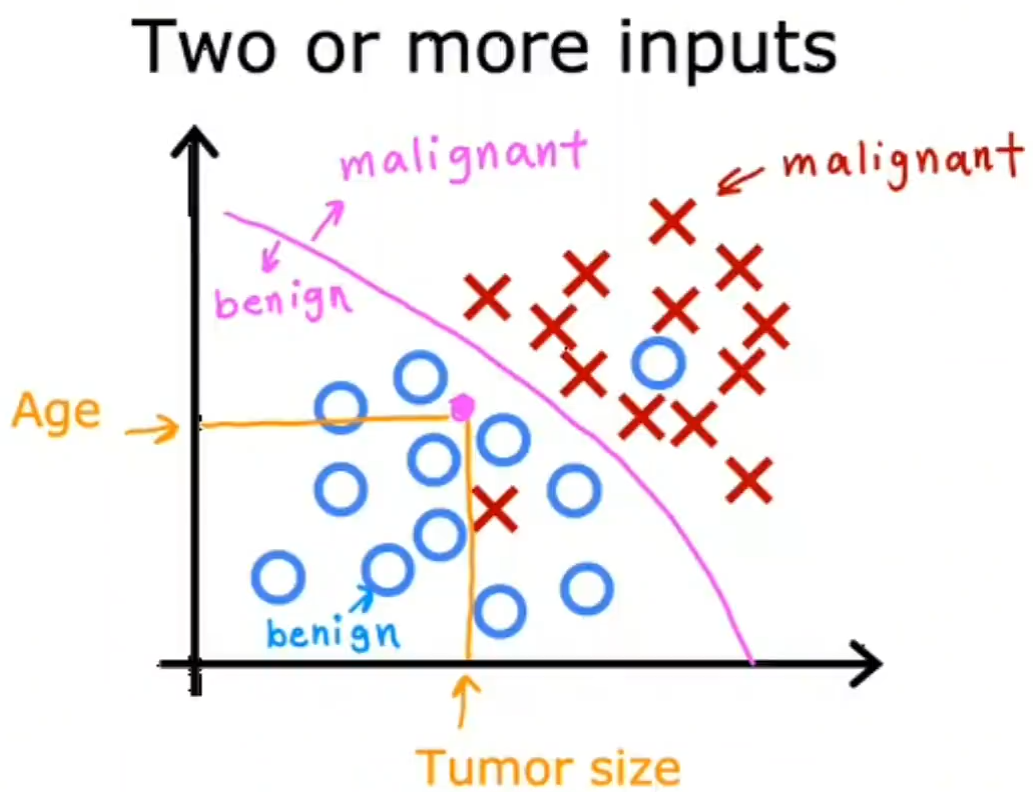
1.3 Unsupervised learning 无监督学习

​ 给定数据仅带有输入x而没有输出标签y，通过算法在数据中找到一定的结构或模式，由算法自己决定如何分组。

Clustering(聚类)
Anomaly detection(异常检测)
Dimensionality reduction(降维)

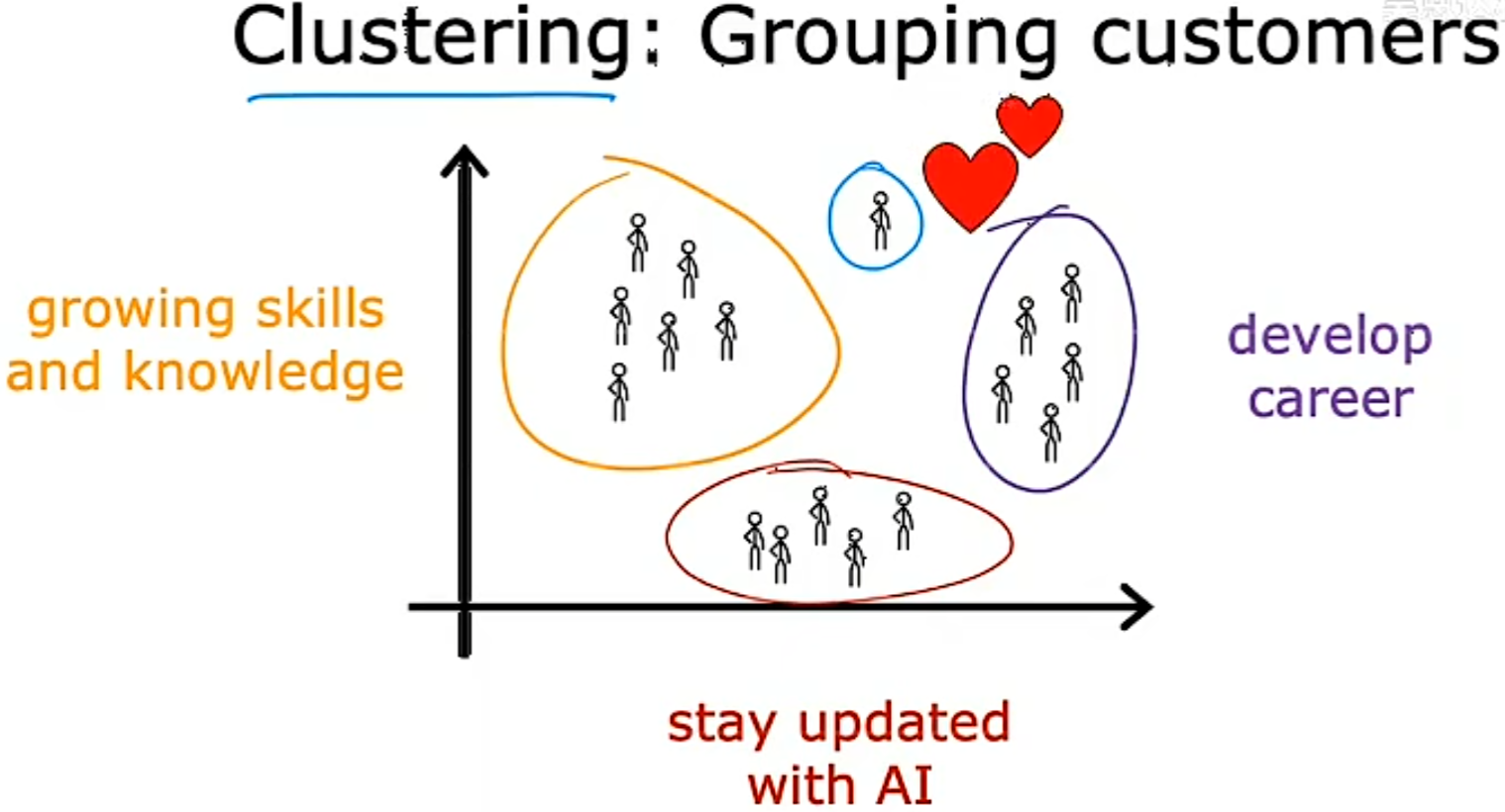
Clustering(聚类) Algorithm:

​ 获取没有标签的数据，并尝试自动将它们分组到集群中。

对用户进行分类，确定其目标用户。

Jupyter Notebooks

pip install jupyterlab
pip install notebook

jupyter lab
jupyter notebook

2.1 Linear Regression(线性回归)

例子：预测房子价格和面积大小的关系，其中每一个数据点对应一个房子的面积与价格的关系，需要回答某一间房子能卖多少钱。模型需要通过数据集画出一个数据拟合后的直线，进而在特定的面积下得到大致对应的预测价格。

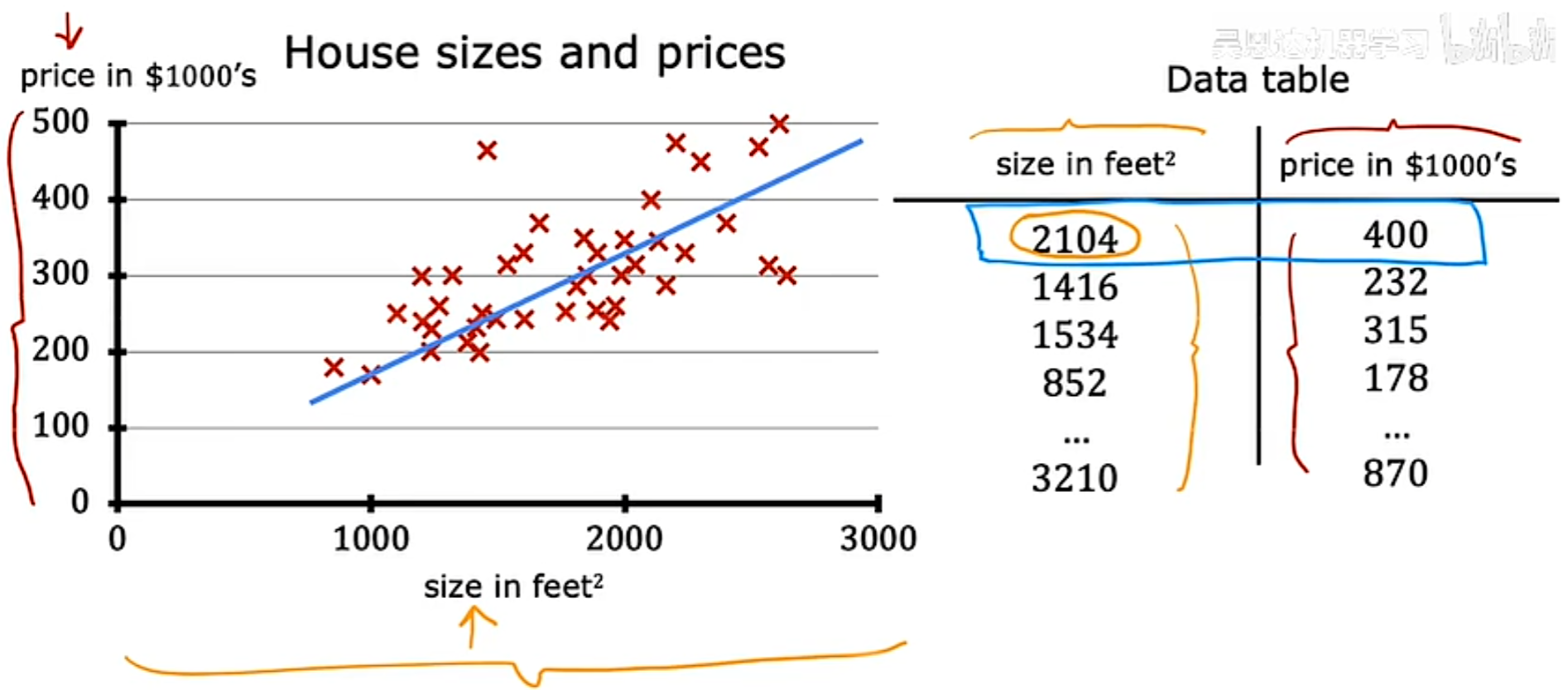
​ 可视化数据除了图表外，还有数据表：

Some Terminology

​ Train set(训练集): Data used to train the model
​ x : “input” variable
​ “input” feature
​ y : “output” variable
​ “target” variable
​ m : number of training examples
​ (x, y) : single training example
​ (x(i) ,y(i)) : i th training example

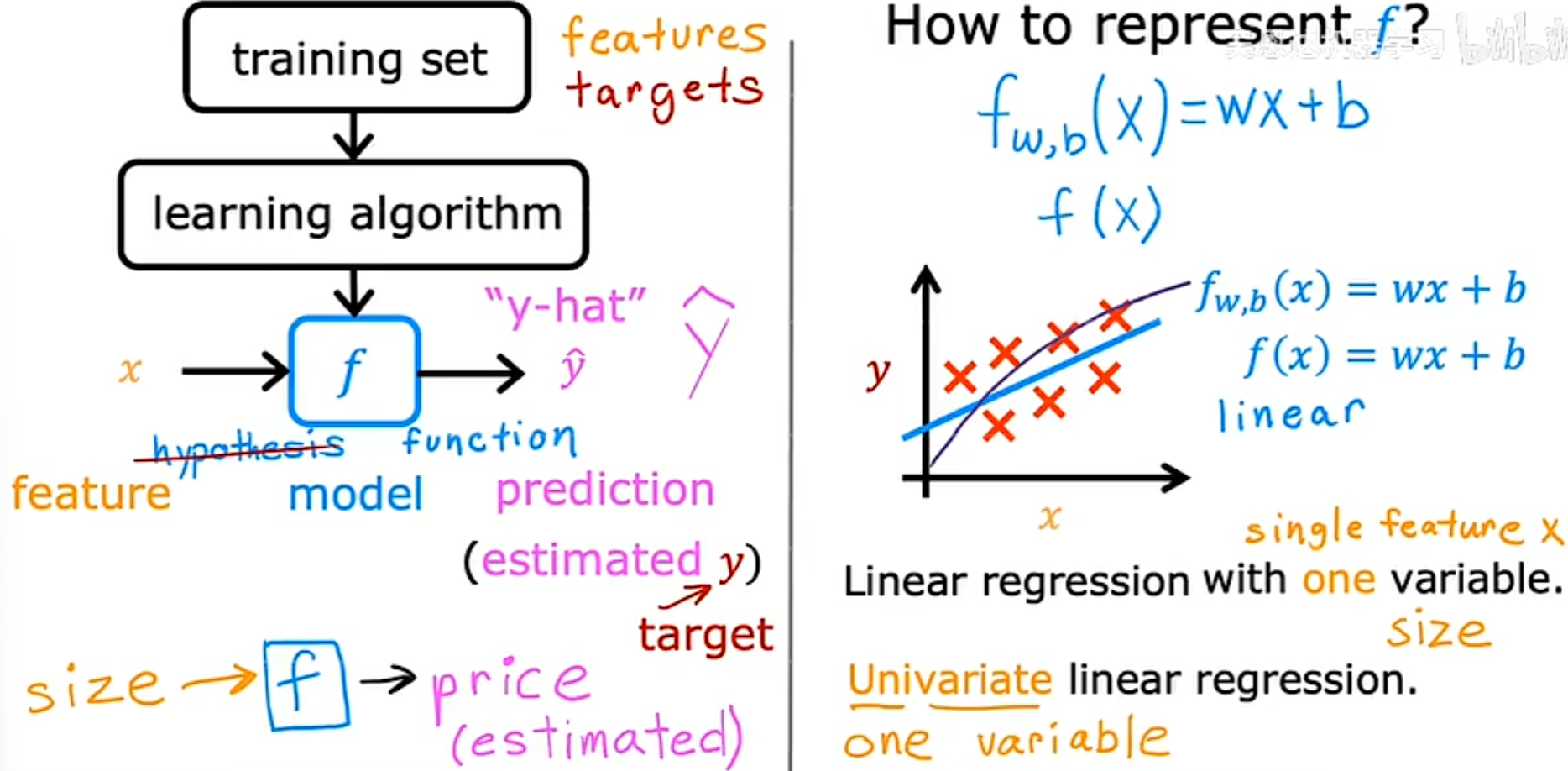
线性回归方程

线性回归方程就是具有只一个变量的线性回归。只具有一个输入变量的线性模型还被称为单变量线性回归(univariate linear regression) 。

为了训练模型，我们需要输入一系列的训练集给学习算法，然后通过监督学习算法，将生成一个方程，假设方程(f)。其工作是通过输入的x，进而得出一个假设的y*(y-hat)*的值。

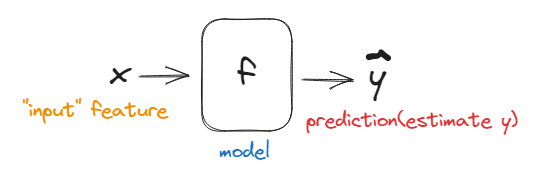
重点是，我们应该如何得到函数f。例如如下函数
$$f(x)=wx+b$$
我们需要得出的重点是，w和b的值是多少

实验代码

一些导入的库

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt # matplotlib.pyplot是一些命令行风格函数的集合，使matplotlib以类似于MATLAB的方式工作。
import seaborn as sns
sns.set(context="notebook", style="whitegrid", palette="deep")	# 初始化一系列参数

A=np.eye(5)   #输出单位对角矩阵
print(A)

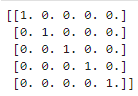
df = pd.read_csv('ex1data1.txt',names=['人口','利润'])    # header = None表示没有表头  
#pd.read_csv的作用是将csv文件读入并转化为数据框形式，有非常多的参数，用到时可查阅文档。

在读取文件后，此时df中应该存放了数据，并且按照将两列数据的内容按列名 人口、利润 进行了区分

读前5行数据：

df.head() #读前5行
#括号内可填写要读取的前n行，如果不填，默认为n=5

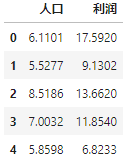
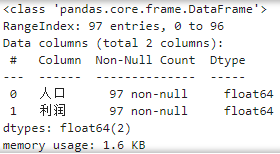
df.info() #查看索引、数据类型和内存信息

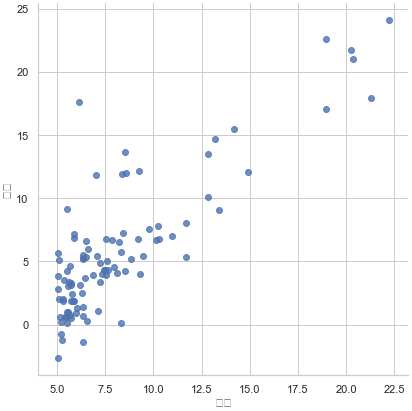
绘制散点图观察原始数据

sns.lmplot('人口','利润',data=df,size=6,fit_reg = False)
#fit_reg:拟合回归参数,如果fit_reg=True则散点图中则出现拟合直线
plt.show()

2.2 Cost Function(代价函数)

代价函数基本定义

代码函数将告诉我们模型的运行情况。

在线性方程中，w和b称为模型的参数，参数是我们在训练期间通过调整来改进模型的变量。

根据所选择的参数的不同，可以得到不同的x的函数f。

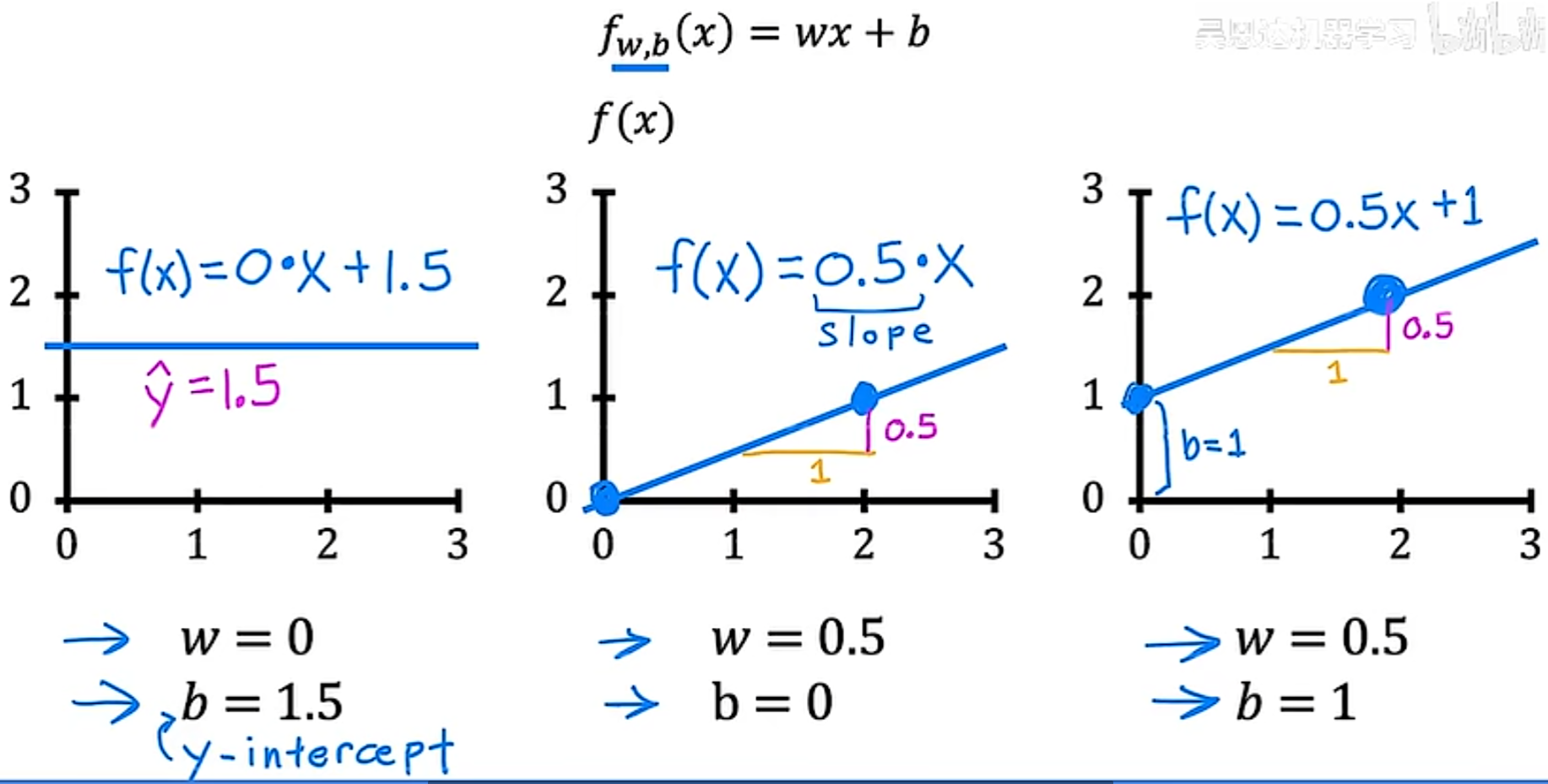
在线性回归中，所要做的是选择参数w和b的值，以便从函数f所获得的直线以某种方式更好的拟合数据。重点问题是，如何找到w和b的值，以便于许多可能的所有训练示例x^i和yi的预测y-hat^{i更接近于真实目标y}i。

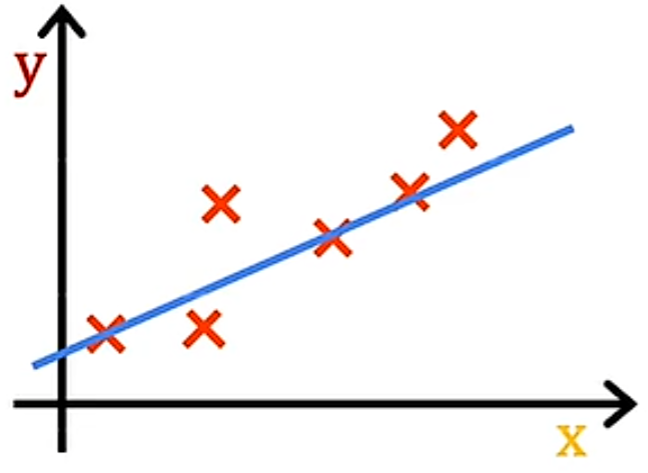
如何衡量一条直线与训练数据的拟合程度？

​ 首先，需要一个代价函数，代价函数会采用预测y-hat并通过取y-hat减去y将其与目标y进行对比。y和h-hat之间的差距成为error(误差)，计算全部误差的平方的和，最后将其除以m，而且，一般机器学习中的成本函数是除以2m，额外的2只是为了让我们后面的计算看起来更整洁

Cost function: Squared error cost function(平方误差成本函数)

tips:
	m = number of training examples

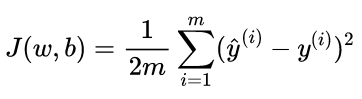
等价于

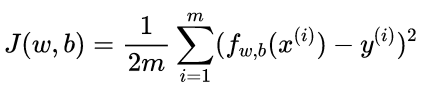
Cost Function Intuition(代价函数直观理解)

​ 目前为止：

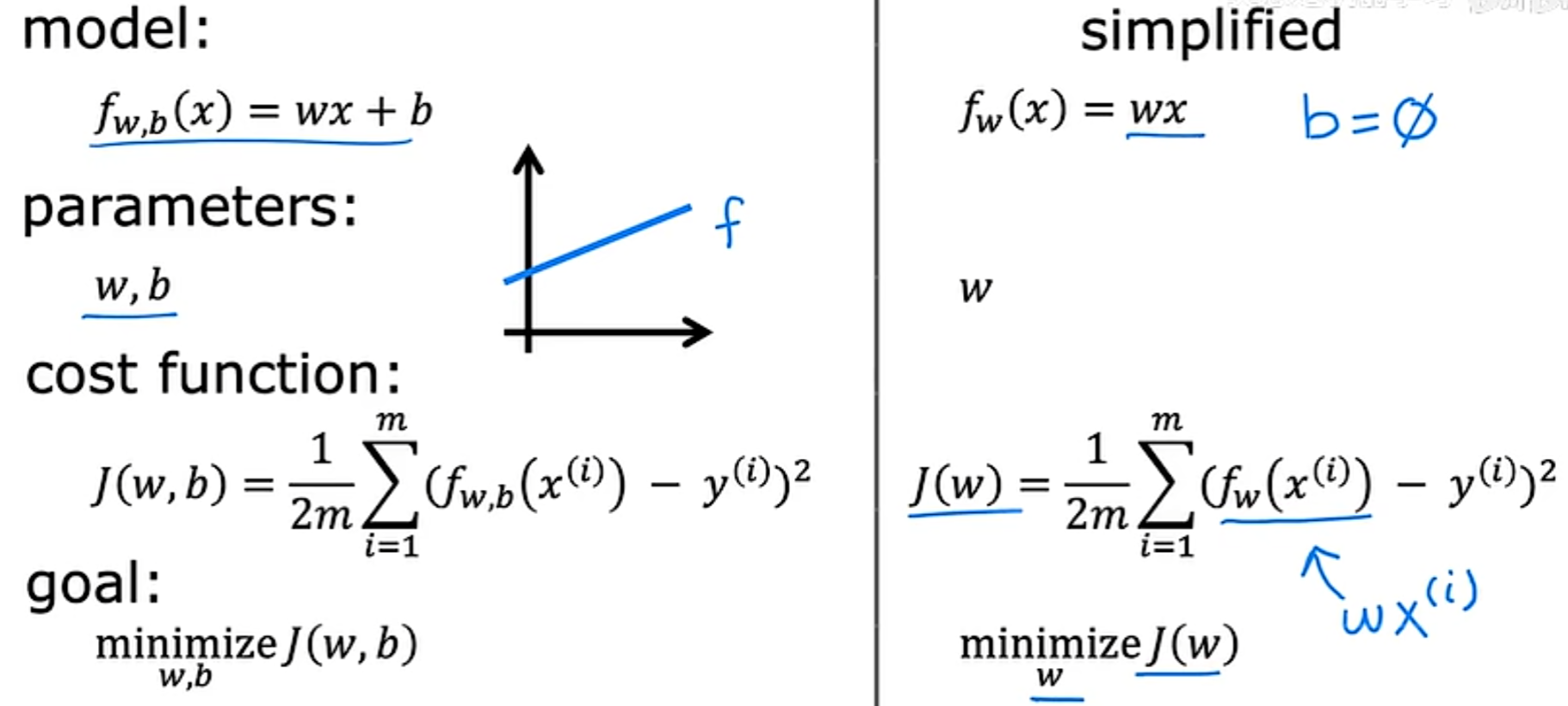
根据已知的f(x)绘制简化后的 J(x) 的图像：

​ 1. 当w=0时，从代价函数的表达式可以看出，J(w) = 0，图像如下

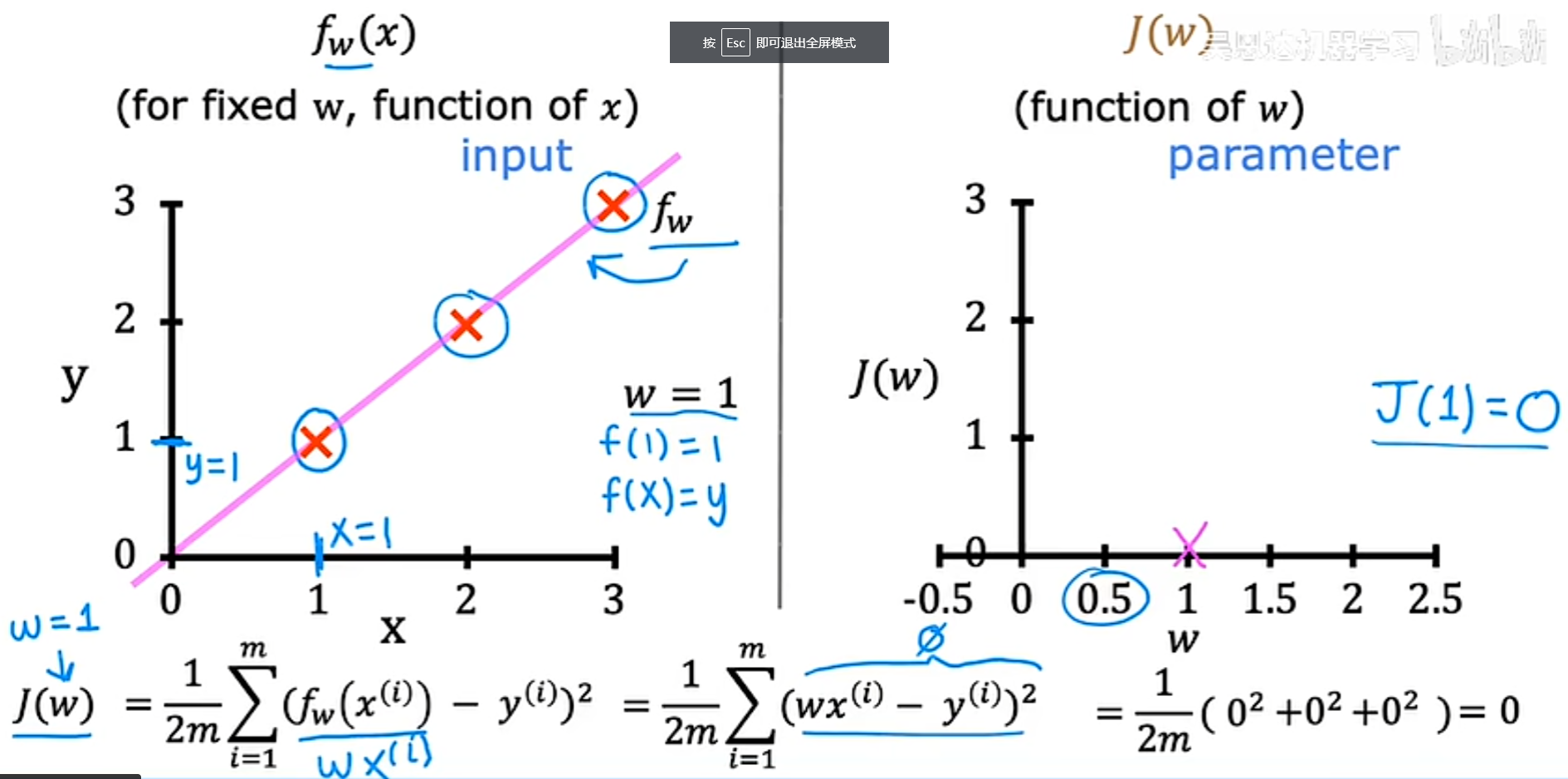
2. 当w=0.5时，同样通过带入代价函数来进行计算得到 J(0.5)约等于0.58，如图

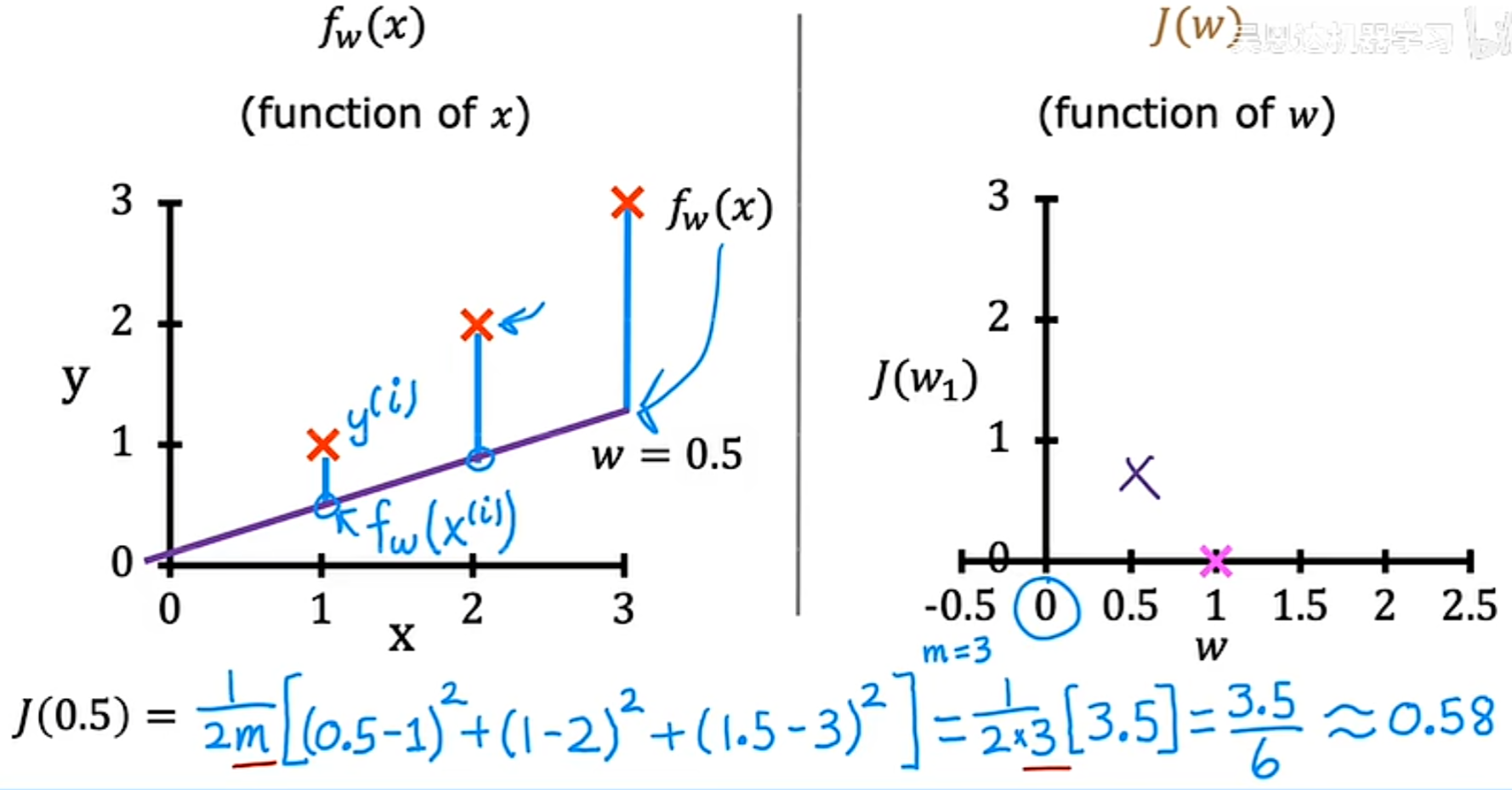
3. 当w=0时，同样，如图

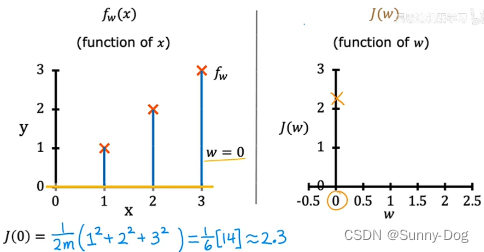
同理，可以取很多w可能的值，进行一系列的计算。对于w的每个值，最终可以得到一条不同的线以及 w 对应的代价函数 J ，进而可以得到代价函数的可视化图像如下所示，从其中可以看到，当w=1时，代价函数最小：

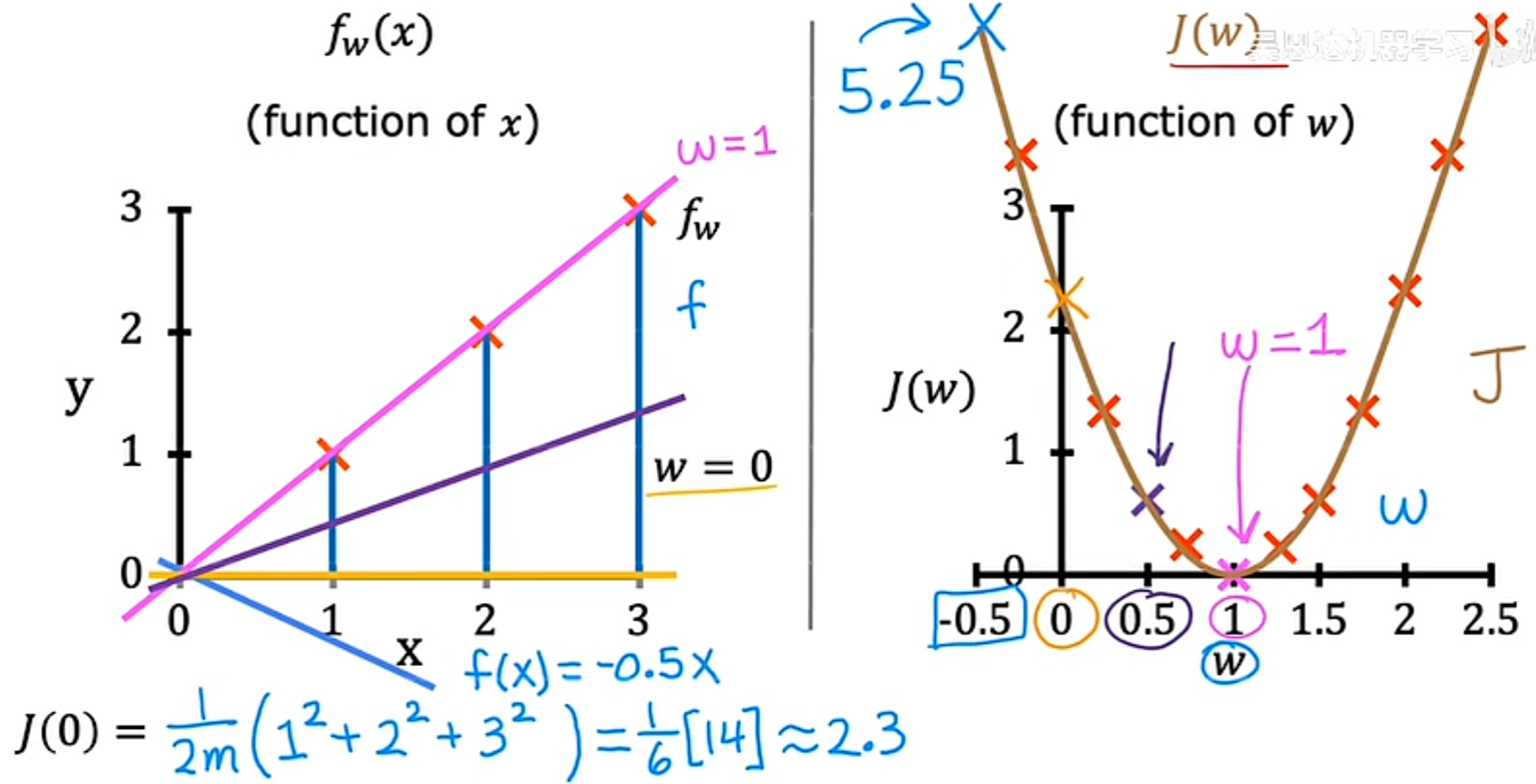
所以，应该如何选择产生函数f的w值，进而更好的拟合数据呢？

答：选择一个使 w 的 J 尽可能小的 w 值

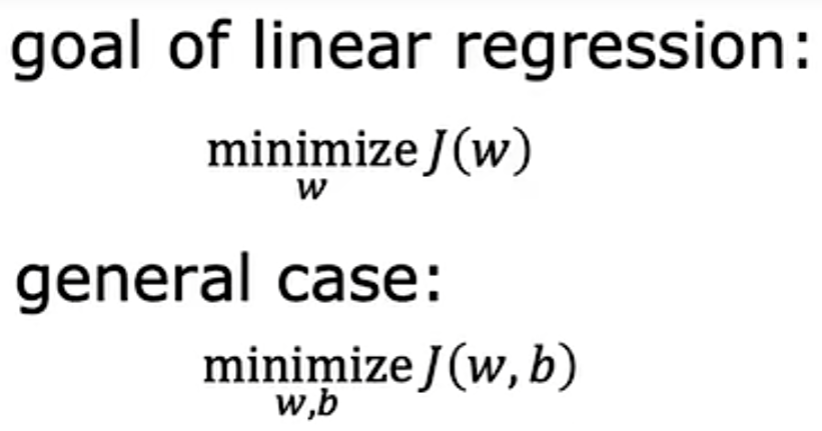
线性回归的目标是：找到参数 w 或 w 和 b，使得承办函数 J 的值最小。

可视化的代价函数

当模型包含 w 和 b 两个参数时，代价函数的可视化图形更像是一个类似碗状的三维图像。

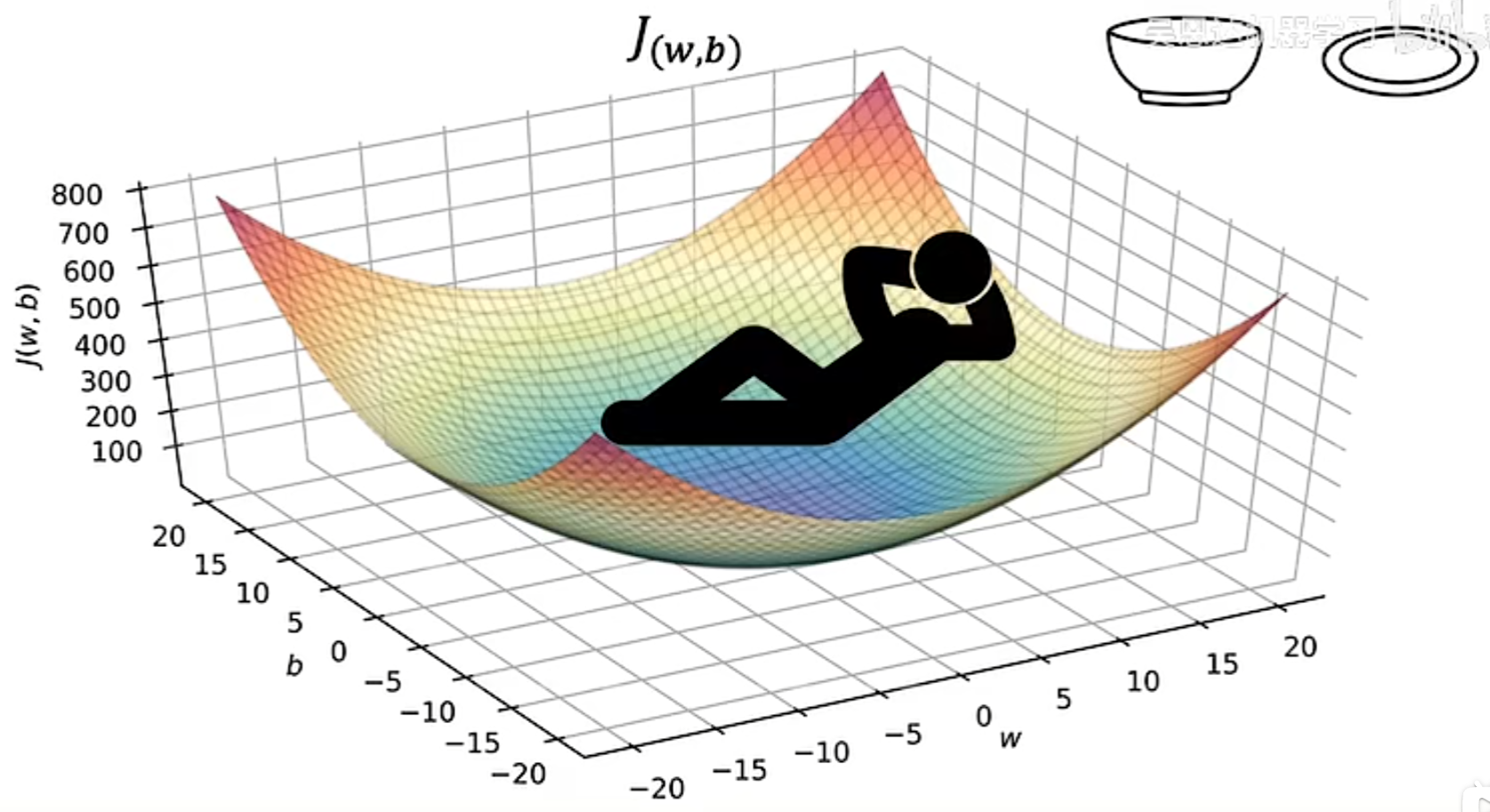
等价函数的另一种图像，等高线图，该图可以看出，三个不同的点所对应的代价函数的值是相同的(等高)。并且，等高线图的中心点，就是等价函数最小的点(mininum)。

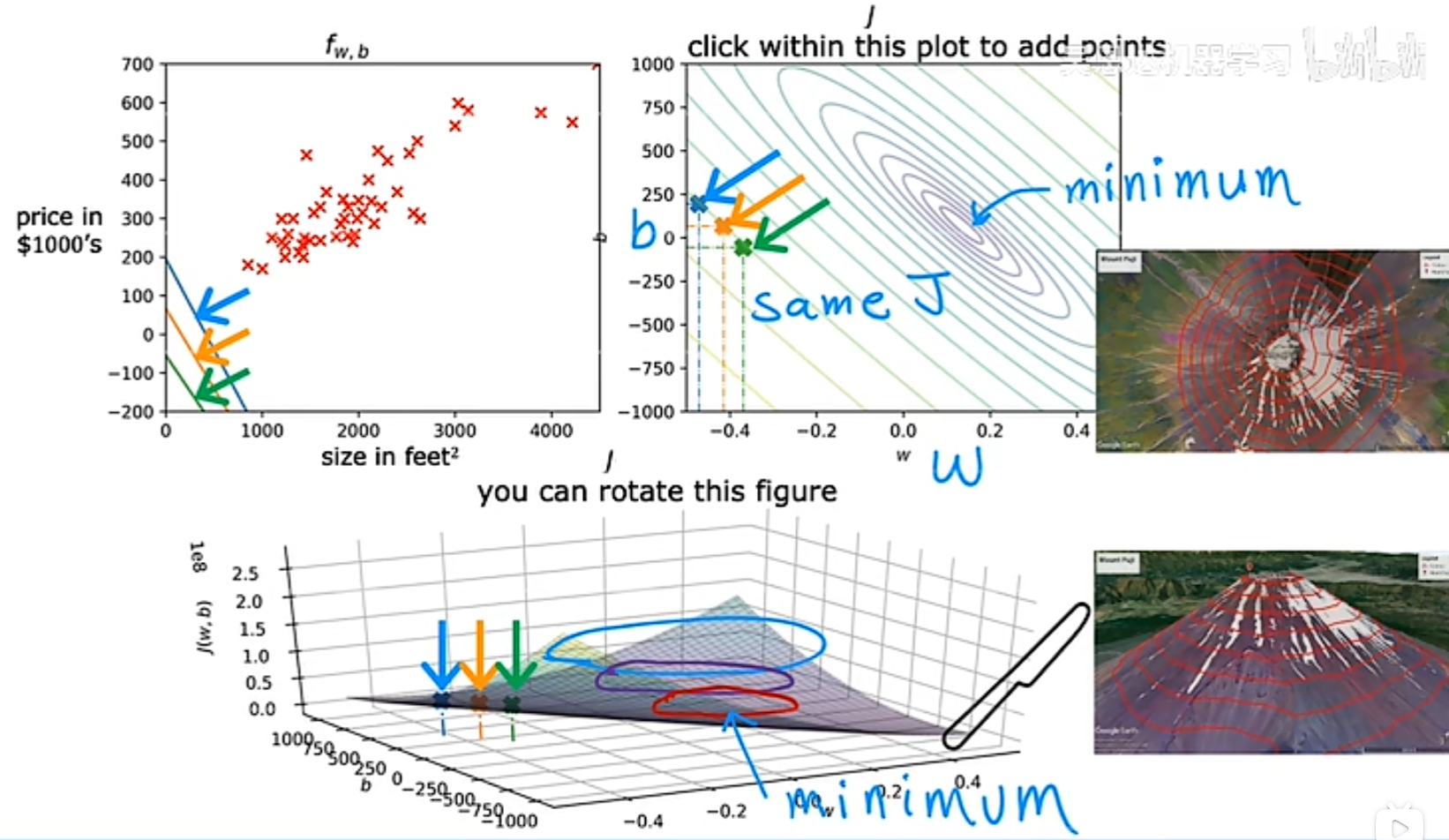
可视化例子

通过不同的 w 和 b 取值的例子，我们可以看出，当最后的代价函数值越靠近中心点的变量取值，他的拟合效果越好：

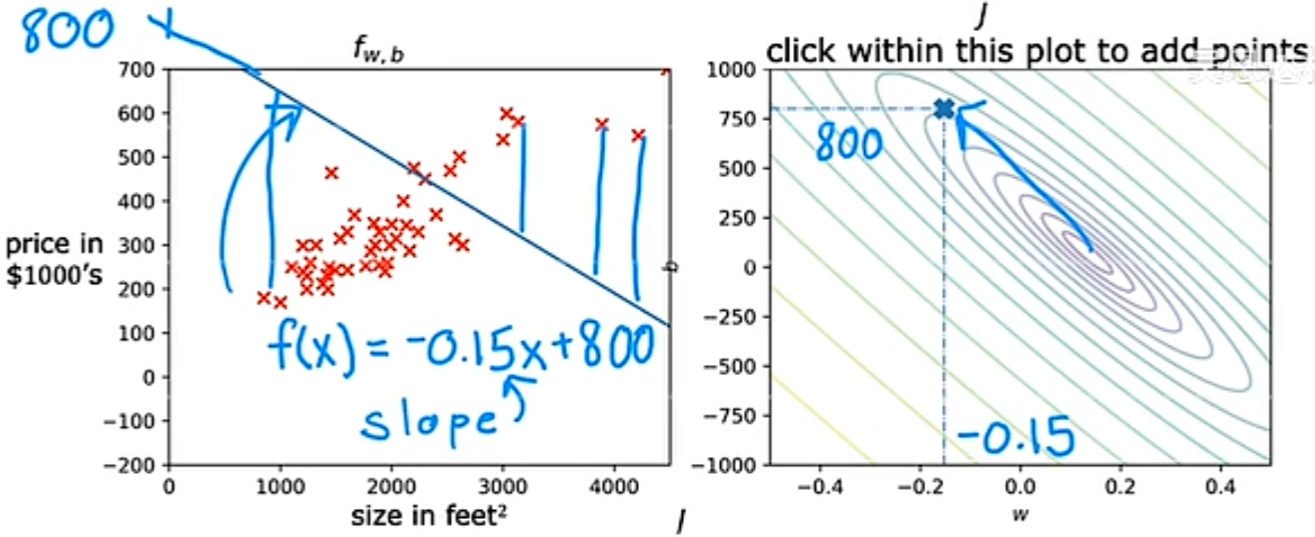
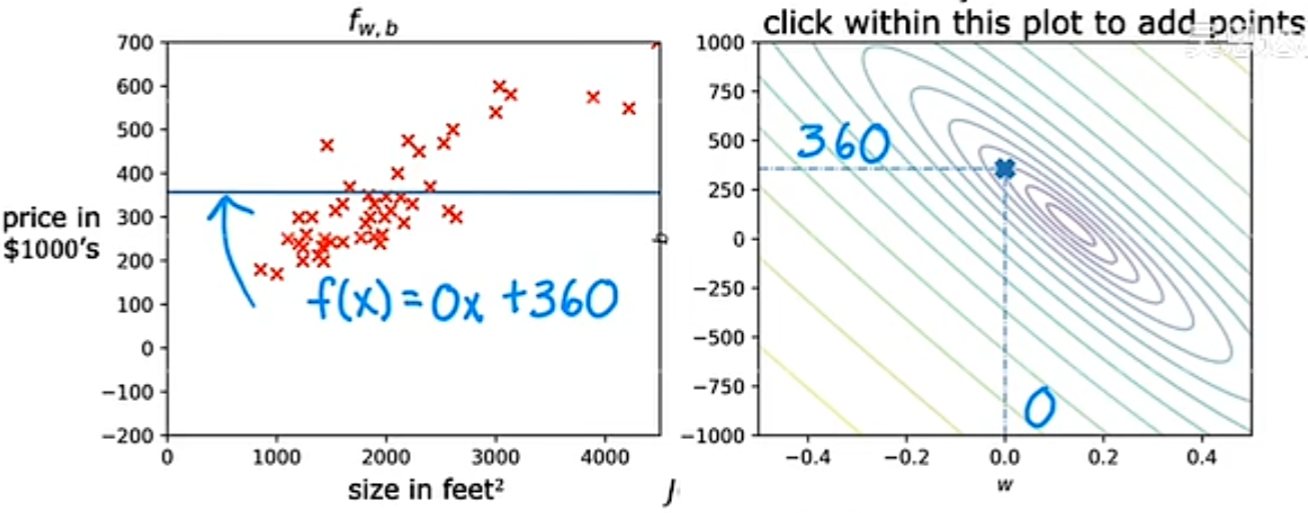
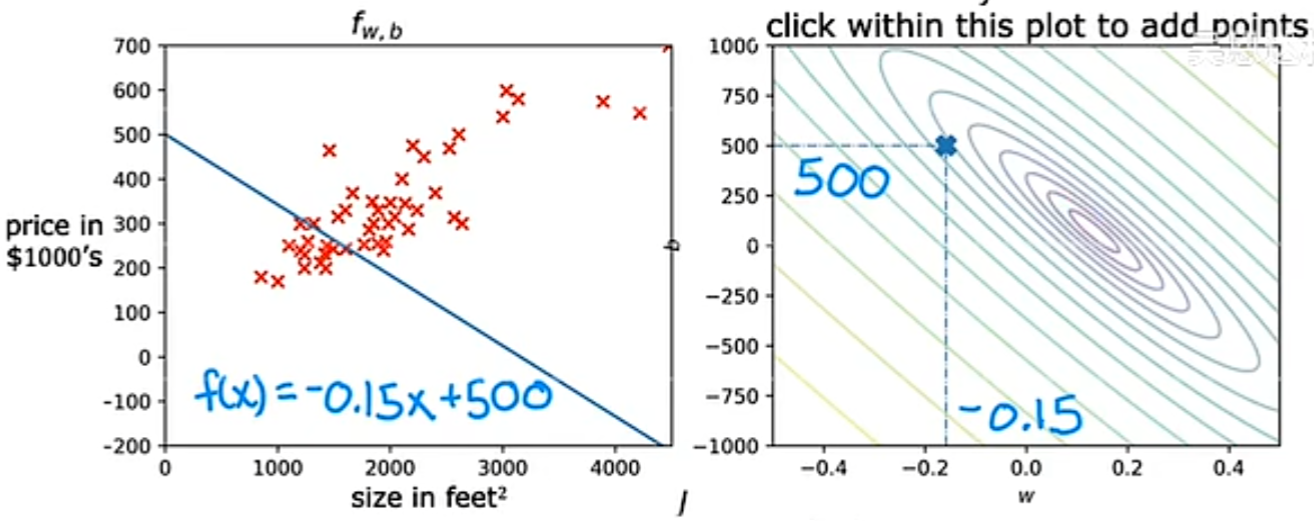
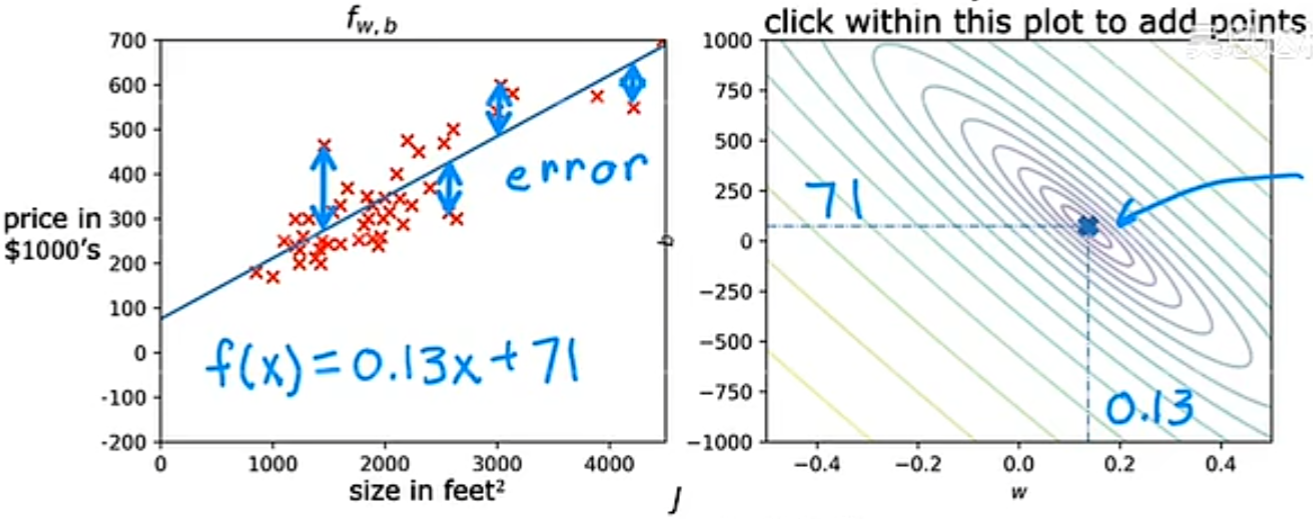
实验代码

代价函数：

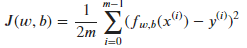
基于代价函数的算式，当模型为：

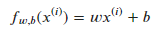
此时的代码实现：

def compute_cost(x, y, w, b): 
    """
    Computes the cost function for linear regression.
    
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    
    Returns
        total_cost (float): The cost of using w,b as the parameters for linear regression
               to fit the data points in x and y
    """
    # number of training examples
    m = x.shape[0] #表示一维数组的长度
    
    cost_sum = 0 
    for i in range(m): 
        f_wb = w * x[i] + b   
        cost = (f_wb - y[i]) ** 2  
        cost_sum = cost_sum + cost  
    total_cost = (1 / (2 * m)) * cost_sum  

    return total_cost

3.1 Gradient Descent(梯度下降)

​ 用于求函数最小值的算法，求代价函数 J(w,b) 的最小值。

​ 使用梯度下降算法，就是设置 w,b 为一个初始值，每次都稍微改变参数 w 和 b 的值以尝试降低 J(w,b) ，直到希望 代价函数 J(w,b) 稳定在或接近最小值。

​ 想象站在一个山上，对于自己的360度的方向，需要选择一个方向迈出一步，确保这一步比其他各个方向下降的都要快，然后到达下一个点后以此类推，最终下降到最低点。并且，如果从不同的(w,b)作为起点，最后降低到的最低点不同，这些谷底被称为local mininum(局部极小值)。

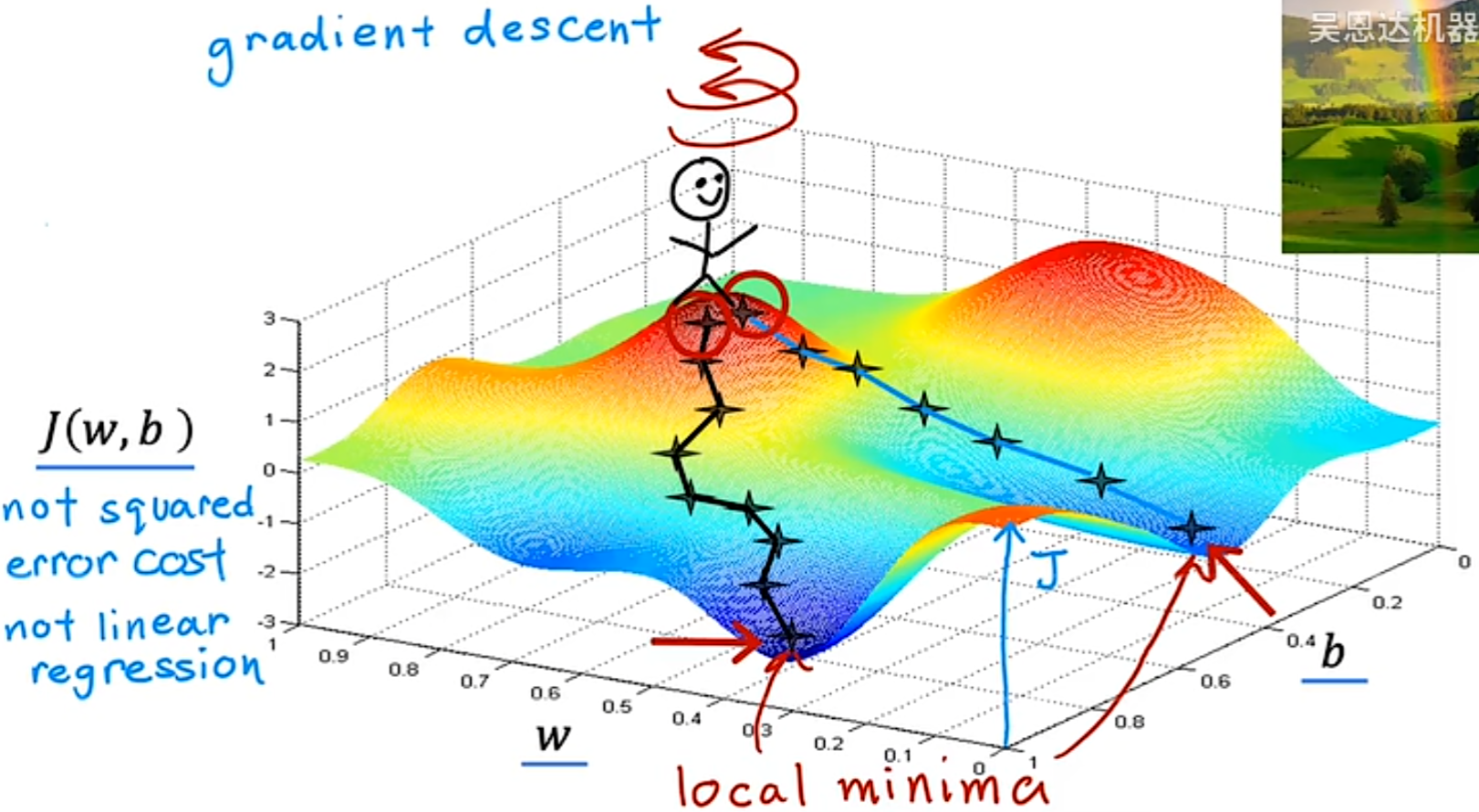
3.2 Implementing Gradient Descent(实现梯度下降)

​ 如前一节中所说的，需要对变量的值一直进行调整，以得到最小的代价函数。因此需要一系列的公式来一步步计算出最合适的w，梯度下降算法公式为：

​ 从公式的理解来看，α表示的是w或b每下降一步的步幅，J(w,b)对于w或d的偏导数则表示下降的方向，就是一步一步下降直到代价函数收敛(到达局部极小值)。但是，我们最希望的是能够同时更新 w 和 b 的值，在同时更新时找到局部极小值,需要以下方式:

3.3 Gradient Descent Intuition

​ 对于梯度下降的函数的直观理解，即是通过函数的导数一步步下降，可以看出代价函数就是沿着图像某点的斜率的方向一步步下降。（其实就是一些微积分的导数部分的内容…）

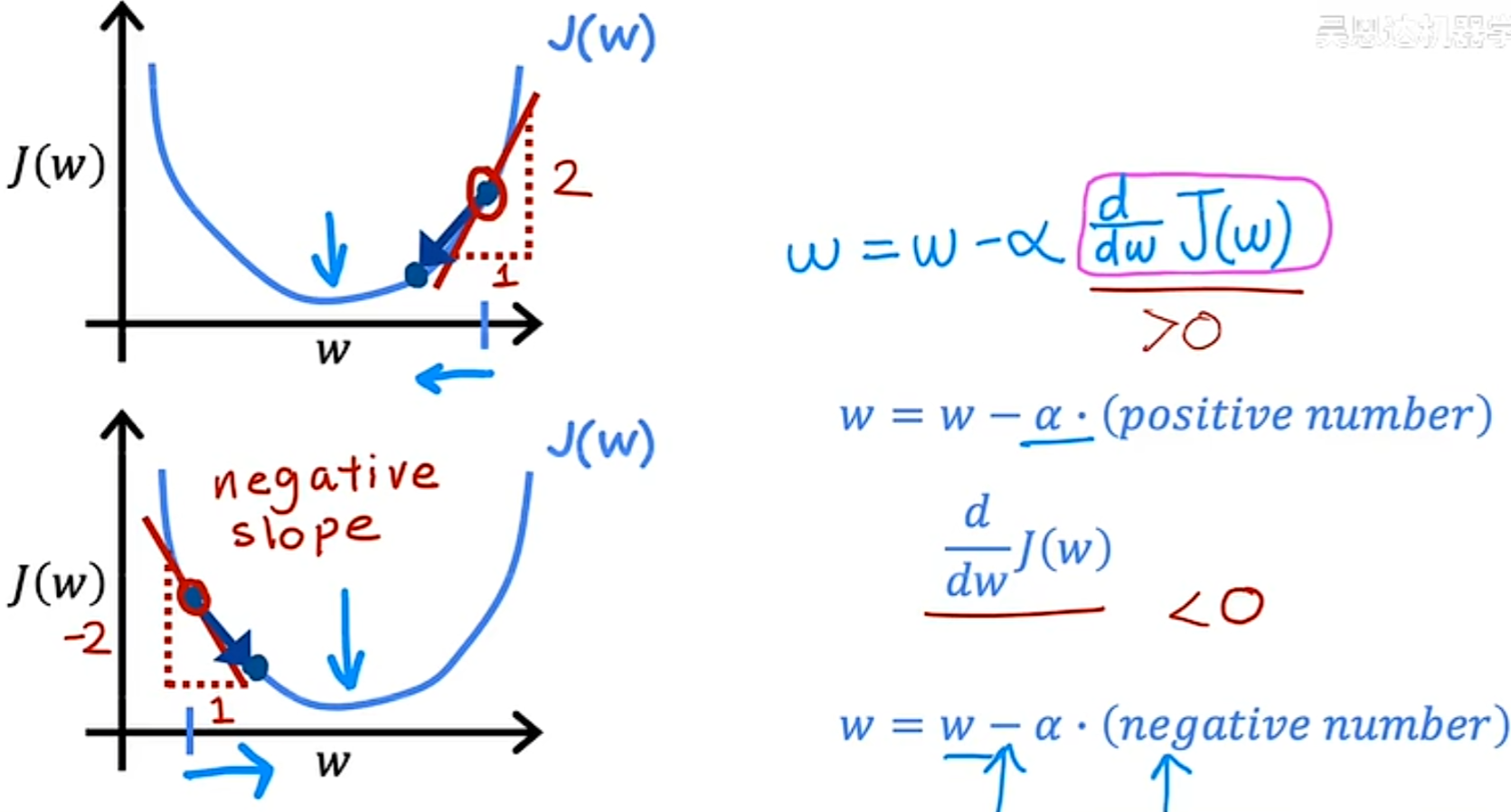
3.4 Learning Rate(学习率)

​ α 的选择在梯度下降中也扮演着重要的角色。

1. 当 α 太小时。每次下降都之迈出很小很小的一步，结果就是最终虽然降低了代价函数，但是计算了很多很多步，速度很慢。

2. 当 α 过大时。可能会导致本来已经很接近最小值的代价函数，反而增大没办法更加靠近最小值。另一种说法是，可能会导致大交叉无法收敛，甚至会发散。

试想一种场景，当此时的w已经到了最小值时，由于在极小值点的斜率为0，也就是说导数为0，因此w的值其实并不会改变。

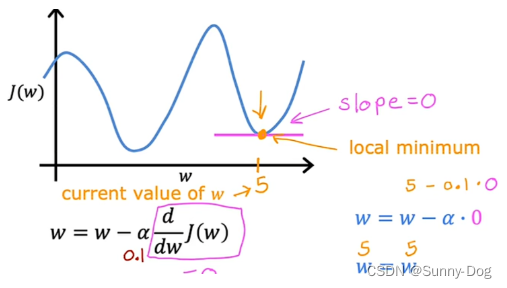
**当学习率(α)固定时，可以达到最小值。**以下是例证：

​ 因为每次下降时，某一点的斜率都会越来越小，在斜率越来越小时，每次减少的值也会越来越小，最终得到最小值。

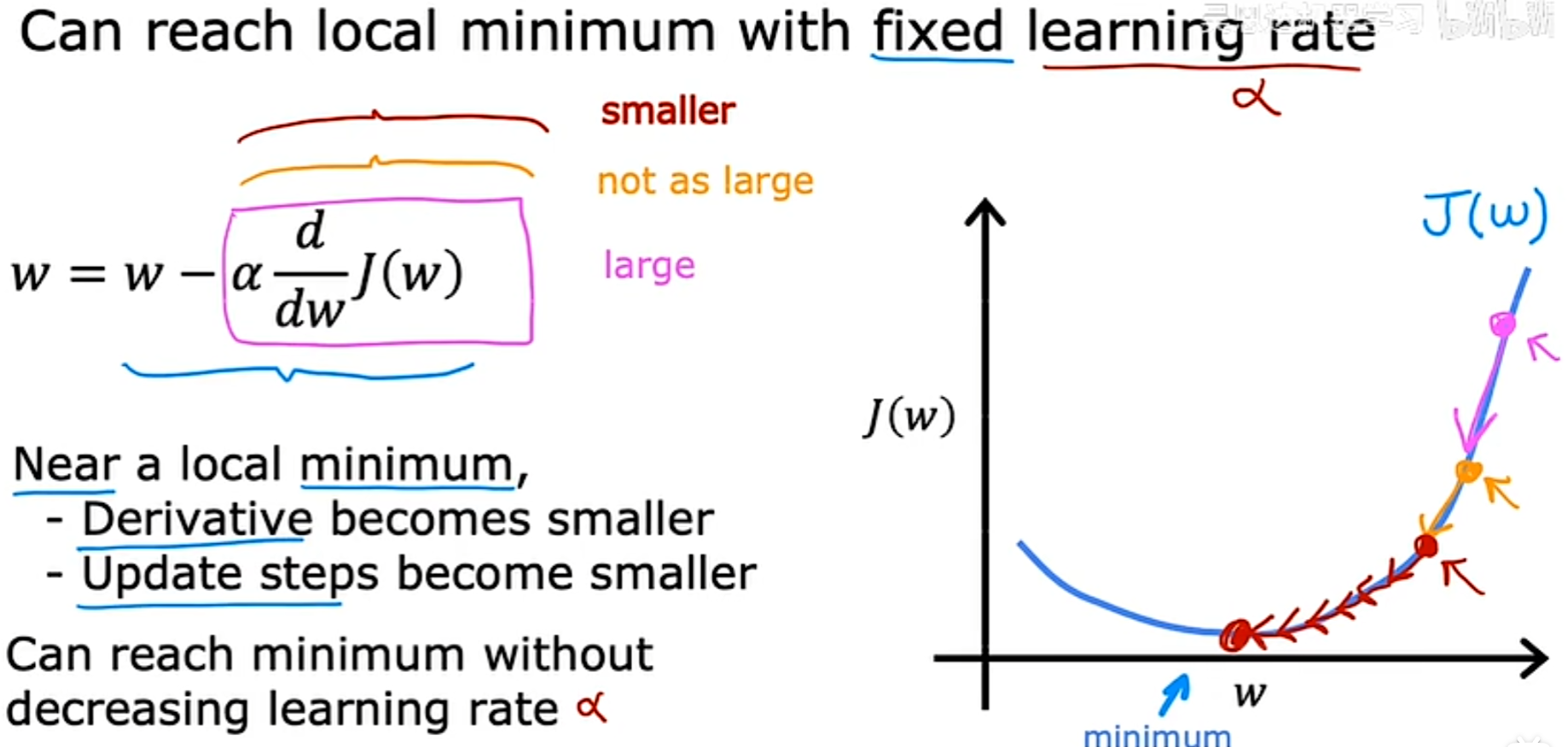
3.5 Gradient Descent for Linear Regression(线性回归中的梯度下降)

联立线性回归算法的模型函数、代价函数以及梯度下降算法，可以得到：

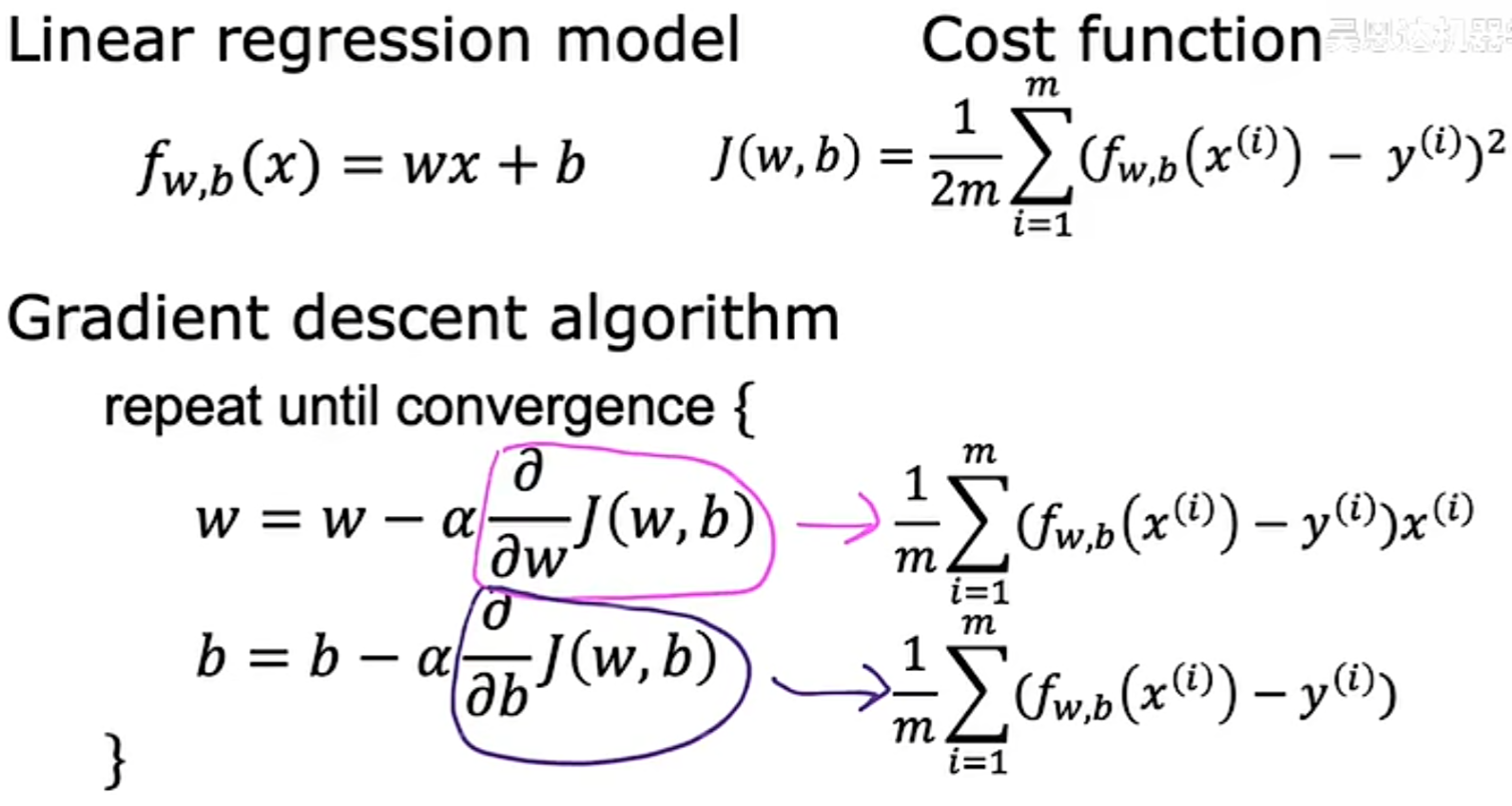
3.6 Running Gradient Descent

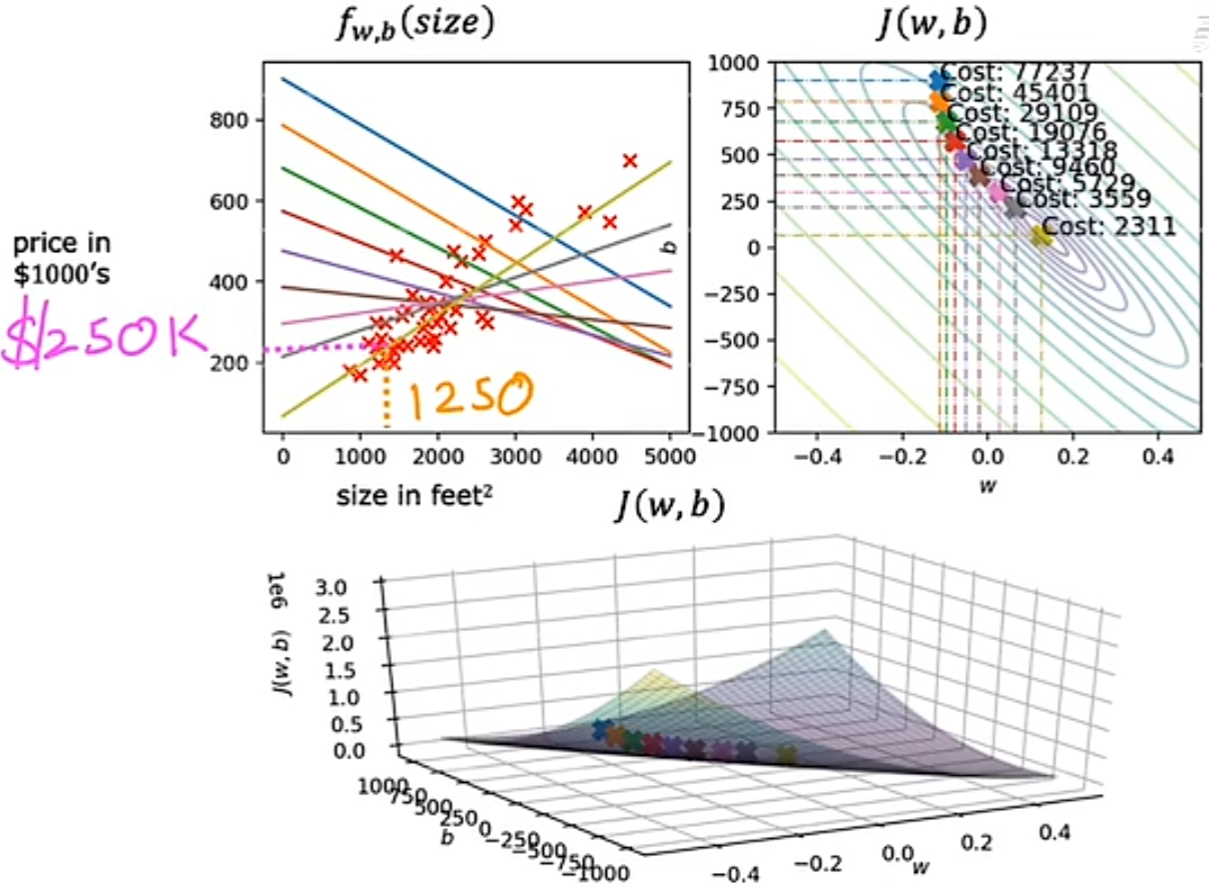
对于这一类的梯度下降，每下降一步都使用所有的训练数据的叫做"Batch" gradient descent。

实验代码

同样，数据集仅两组数据

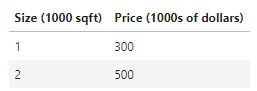
对其进行导入

# Load our data set
x_train = np.array([1.0, 2.0])   #features
y_train = np.array([300.0, 500.0])   #target value

代价函数方程：

#Function to calculate the cost
def compute_cost(x, y, w, b):
   
    m = x.shape[0] 
    cost = 0
    
    for i in range(m):
        f_wb = w * x[i] + b
        cost = cost + (f_wb - y[i])**2
    total_cost = 1 / (2 * m) * cost

    return total_cost

接下来就是梯度下降部分，此处选择线性方程来进行预测：

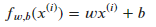
对于该线性方程，所选择的代价函数：

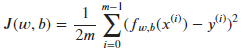
在梯度下降算法中，w和b的更新方式：

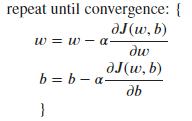
其中：

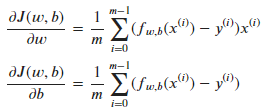
代码部分：

对于梯度的计算，也就是求偏导后的代价函数如下，此处w和b的初始值都取为0：

def compute_gradient(x, y, w, b): 
    """
    Computes the gradient for linear regression 
    Args:
      x (ndarray (m,)): Data, m examples 
      y (ndarray (m,)): target values
      w,b (scalar)    : model parameters  
    Returns
      dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
      dj_db (scalar): The gradient of the cost w.r.t. the parameter b     
     """
    
    # Number of training examples
    m = x.shape[0]    
    dj_dw = 0
    dj_db = 0
    
    for i in range(m):  
        f_wb = w * x[i] + b 
        dj_dw_i = (f_wb - y[i]) * x[i] 
        dj_db_i = f_wb - y[i] 
        dj_db += dj_db_i
        dj_dw += dj_dw_i 
    dj_dw = dj_dw / m 
    dj_db = dj_db / m 
        
    return dj_dw, dj_db

对于梯度下降函数：

def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function): 
    """
    Performs gradient descent to fit w,b. Updates w,b by taking 
    num_iters gradient steps with learning rate alpha
    
    Args:
      x (ndarray (m,))  : Data, m examples 
      y (ndarray (m,))  : target values
      w_in,b_in (scalar): initial values of model parameters  
      alpha (float):     Learning rate
      num_iters (int):   number of iterations to run gradient descent
      cost_function:     function to call to produce cost
      gradient_function: function to call to produce gradient
      
    Returns:
      w (scalar): Updated value of parameter after running gradient descent
      b (scalar): Updated value of parameter after running gradient descent
      J_history (List): History of cost values
      p_history (list): History of parameters [w,b] 
      """
    
    w = copy.deepcopy(w_in) # 通过深复制方式给w赋值，避免修改初始值w_in
    # 用于存储每次迭代的代价函数和 J 和 参数 w，用于后续绘图
    J_history = []
    p_history = []
    b = b_in
    w = w_in
    
    for i in range(num_iters):
        # 用 gradient_function 计算梯度并更新参数
        dj_dw, dj_db = gradient_function(x, y, w , b)     

        # 用学习率更新参数
        b = b - alpha * dj_db                            
        w = w - alpha * dj_dw                            

        # 保存每次迭代的cost
        if i<100000:      # prevent resource exhaustion 
            J_history.append( cost_function(x, y, w , b))
            p_history.append([w,b])
        # 每隔10次打印一次cost，如果<10次，则打印多次cost
        if i% math.ceil(num_iters/10) == 0:
            print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
                  f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e}  ",
                  f"w: {w: 0.3e}, b:{b: 0.5e}")
 
    return w, b, J_history, p_history #return w and J,w history for graphing

运行：

# initialize parameters
w_init = 0
b_init = 0
# some gradient descent settings
iterations = 10000
tmp_alpha = 1.0e-2
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha, iterations, compute_cost, compute_gradient)
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")

得到最终的w和b，并且可以观察到过程中w、b以及J在每迭代1000次后的变化：

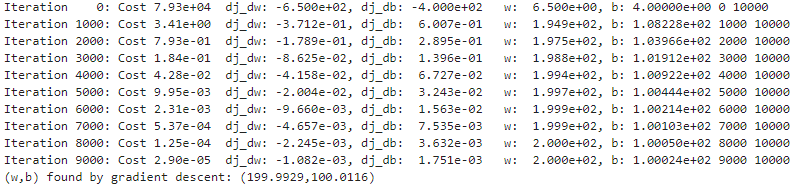
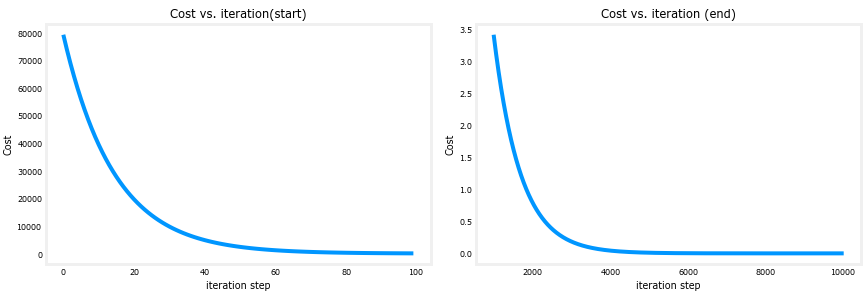
在课程内有提到，由于在代价函数不断减小的过程中，其图像斜率不断减小，因此到最后每次减小的幅度也会下降。

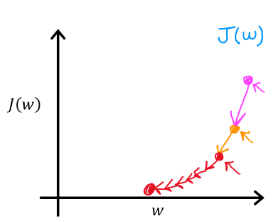
这一过程可以通过绘图直观感受：

# plot cost versus iteration  
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))
ax1.plot(J_hist[:100])
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])
ax1.set_title("Cost vs. iteration(start)");  ax2.set_title("Cost vs. iteration (end)")
ax1.set_ylabel('Cost')            ;  ax2.set_ylabel('Cost') 
ax1.set_xlabel('iteration step')  ;  ax2.set_xlabel('iteration step') 
plt.show()