机器学习笔记【二】逻辑回归与分类(2):感知机学习算法与逻辑回归的区别,牛顿方法
本节为吴恩达教授机器学习笔记第二部分:逻辑回归与分类(2)-感知机学习算法与逻辑回归的区别,牛顿方法。2. 感知机学习算法与逻辑回归的区别 区别1:这两位都是线性分类器,但是逻辑回归使用对数损失函数,而感知机使用的是均方损失函数(即错误点到分离平面的距离,最小化该值)。 区别2:逻辑回归的激活函数也与感知机不同,前者是sigmoid函数,后者是一个阶跃函数: 这就导致逻辑回归连续可导,使得最
本节为吴恩达教授机器学习笔记第二部分:逻辑回归与分类(2)-感知机学习算法与逻辑回归的区别,牛顿方法。
2. 感知机学习算法与逻辑回归的区别
区别1:这两位都是线性分类器,但是逻辑回归使用对数损失函数,而感知机使用的是均方损失函数(即错误点到分离平面的距离,最小化该值)。
区别2:逻辑回归的激活函数也与感知机不同,前者是sigmoid函数,后者是一个阶跃函数: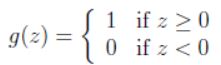
这就导致逻辑回归连续可导,使得最终结果有了概率解释的能力。而阶跃函数是一个分段函数非0即1,分类粗糙。
那问题又来了,针对第一个区别,为什么逻辑回归不能用均方损失左损失函数呢?
我们设想可以,则优化的目标函数为: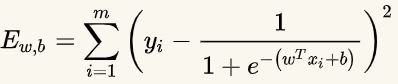
这个目标函数是非凸的,不容易求解,会得到局部最优。而用极大似然,对数似然函数是高阶连续可导凸函数,方便用梯度下降或者牛顿方法等凸优化方法来进行优化。
此外,综合线性回归,逻辑回归和感知机学习。
- 感知机算法仅在线性可分条件下有效,非线性则需要pocket算法
- 线性回归容易优化,在0/1错误下对于|ys|有比较宽松的VC维界
- 逻辑回归同样容易优化,在0/1错误下对于 y s < < 0 ys<<0 ys<<0有比较宽松的VC维界
这里问题又来了,啥是VC维界,详细可以这篇文章解读机器学习基础概念:VC维的来龙去脉,简单来说就是VC维反映了假设空间的强大程度。VC维越大,H越强,即可以打散更多的点。
3. 牛顿方法
该节介绍了另一种最大化对数似然函数的方法,牛顿方法,它本质上是近似求解方程根的方法,对参数的更新规则如下,找到某个 θ \theta θ使得 f ( θ ) = 0 f(\theta)=0 f(θ)=0,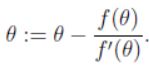
如果要最大化目标函数,可以令: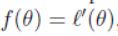
即最大值时一阶导数为0,得到新的参数更新规则: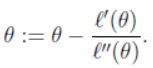
因为逻辑回归中的参数 θ \theta θ时向量,所以进一步对牛顿方法进行推广到多维,得到牛顿-拉夫森方法: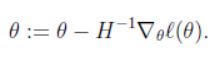
其中, ∇ θ l ( θ ) \nabla_{\theta}l(\theta) ∇θl(θ)表示偏导, H H H是 n × n n \times n n×n矩阵,称为Hessian矩阵: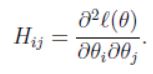
牛顿方法收敛速度优于梯度下降,但是需要计算的Hessian矩阵,所以只要 n n n的值比较小,牛顿方法就更好。使用牛顿方法最大化对数似然函数的方法也称为Fisher scoring。
欢迎扫描二维码关注微信公众号 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读,算法和其他互联网技能的学习,概率论、线性代数等高等数学知识的回顾]
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)