机器学习——神经网络(五):BP神经网络解决异或问题
BP神经网络解决异或问题BP神经网络的推导、python实现代码及结果视图请移至机器学习——神经网络(四):BP神经网络单层感知器异或问题请移至机器学习——神经网络(二):单层感知机异或问题python 3.6numpy、matplotlib库import numpy as npimport matplotlib.pyplot as plt# 载入数据x_data = np.array([[1,0
·
BP神经网络解决异或问题
BP神经网络的推导、python实现代码及结果视图请移至机器学习——神经网络(四):BP神经网络
单层感知器异或问题请移至机器学习——神经网络(二):单层感知机异或问题
python 3.6
numpy、matplotlib库
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
x_data = np.array([[1,0,0],
[1,0,1],
[1,1,0],
[1,1,1]])
y_data = np.array([[0],
[1],
[1],
[0]])
# 初始化权值,取值范围为-1~1
v = (np.random.random([3,4])-0.5)*2
w = (np.random.random([4,1])-0.5)*2
# 学习率
lr = 0.11
# 激活函数
def sigmoid(x):
'''sigmoid函数作为激活函数'''
return 1/(1+np.exp(-x))
def d_sigmoid(x):
'''相对误差对输出和隐含层求导'''
return x*(1-x)
def update():
'''
向后传输,后反馈更新权值的大小
'''
global x_data,y_data,w,v,lr
# 正向计算隐含层和输出层的对应输出
L1 = sigmoid(np.dot(x_data,v)) #隐含层的输出4*4矩阵
L2 = sigmoid(np.dot(L1,w)) #输出层的实际输出4*1
# 计算输出层和隐含层的误差,然后求取更新量
L2_delta = (y_data-L2)*d_sigmoid(L2) # y_data 4*1 矩阵
L1_delta = L2_delta.dot(w.T)*d_sigmoid(L1)
# 更新输入层到隐含层的权值和隐含层到输出层的权值
w_c = lr*L1.T.dot(L2_delta)
v_c = lr*x_data.T.dot(L1_delta)
w = w+w_c
v = v+v_c
def judge(x):
if x>=0.5:
return 1
else:
return 0
if __name__=='__main__':
for i in range(20000):
update() #更新权值
if i%500==0:
plt.scatter(i,np.mean(np.abs(y_data-L2)))
plt.title('Error Curve')
plt.xlabel('iteration')
plt.ylabel('Error')
plt.show()
print(L2)
for i in map(judge,L2):
print(i)
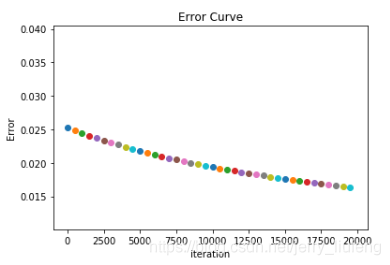
迭代误差图:
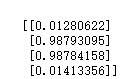
输出结果:
明显可见输出的结果在一定的误差条件下可以看做是:序列[0 1 1 0]
近似输出结果:
使用BP神经网络训练得到的结果与实际的结果相符合,解决了单层感知机中的异或问题。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容

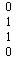







所有评论(0)