量子力学基本概念

薛定谔的猫作为一个通俗易懂的“亲民”实验而被人们所熟知，它向人们搭建了现实世界通往量子世界的桥梁，而细究此实验背后的数学逻辑——线性代数非常精妙的可叠加、可数乘的性质，是深度理解量子力学理论体系的突破口。因此我们可以先尝试理解一些，线性代数与量子力学之间概念的联系。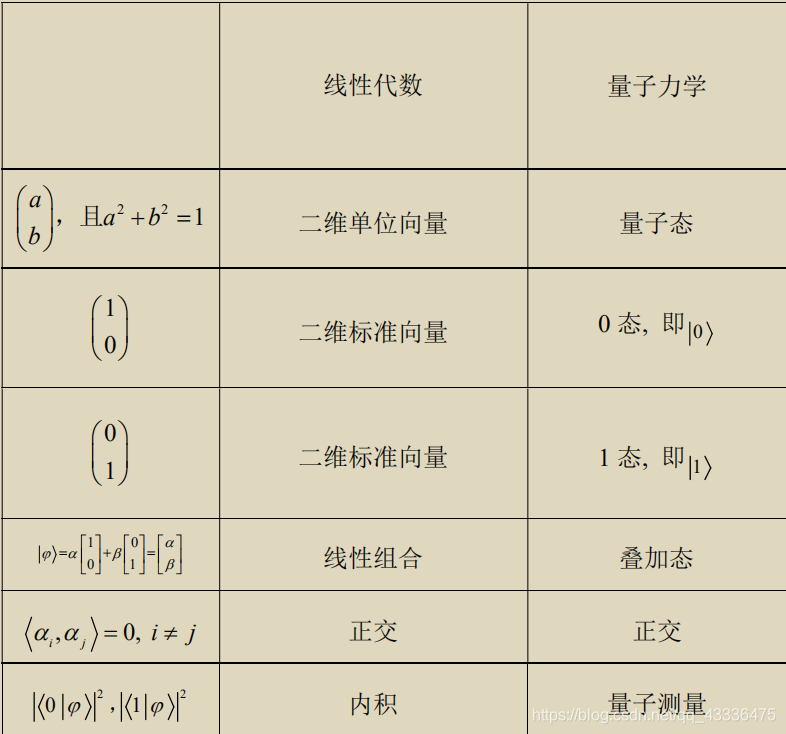

量子：是一个数学概念，“离散变化的最小单元”
离散变化是微观世界的一个本质特征，包括两类：①物质组成的离散变化 ②物理量的离散变化

先看第一类①物质组成的离散变化。例如光是由一个个光子组成的, 不能分出半个光子、1/3 个光子, 所以光子就是光的量子. 再比如, 阴极射线是由一个个电子组成的, 不能分出半个电子、1/3 个电子, 所以电子就是阴极射线的量子。

原子、电子、质子、中子、中微子这些词本身就对应某些粒子, 而“量子”这个词在不同的语境下对应不同的粒子(如果它对应粒子的话). 并没有某种粒子专门叫做“量子”！

再看第二类②物理量的离散变化。例如氢原子中电子的能量只能去-13.6/n^2 eV,n=1,2…,而不能取其他值，像-10eV，-20eV这种，这种离散变化的物理量是微观世界的一个本质特征。
量子力学这个名称其实是为了强调离散变化在微观世界中的普遍性。量子力学出现后, 人们把传统的牛顿力学称为“经典力学”。

态矢量（eigen vector）：表示量子力学状态的矢量，用Hilbert空间中的列单位向量（Hilbert空间我们之后再进行探索）描述，用符号

表示态矢量，可以理解为数学中的向量，一个既有方向又有大小的量

经典位（比特）：用二进制0、1表示两个状态完全不同
在Hilbert空间中，经典比特的0、1可以用一对正交归一的量子态表示

那么，再此二位Hilbert空间中，某个叠加态就可以写为这两个量子态作为基底的线性组合

其中 α 和 β 是复数(之后我们会详细介绍它为复数的原因), 也叫作概率幅或者几率幅, 并且满足α|²+|β|²=1，|α|²、|β|²分别表示叠加态坍缩到0和1的概率. 这样的一个态被称为量子比特。
量子比特（quantum bit 简称为qunbit）：一个可以在二维复数 Hilbert 空间中描述的两能级量子体系，根据叠加原理，量子比特的任何态都可以写成如下形式:

对于经典比特与量子比特之间的联系与差别，我们可以视经典比特为一个普通开关只有开与关两种状态，量子比特为旋钮开关，就像热水器开关一样可以处于[0,100]中的任意一个状态。所以量子比特比经典比特包含更多的信息。

叠加态的可能性是量子力学所有怪异之处的根源. 假如用 0 代表你在北京喝茶, 1 代表你在四川打麻将, 那么这个式子：

就意味着你同时在北京喝茶与四川打麻将！这种状态在现实中怎么可能存在呢？但量子力学的一切实验结果都表明, 叠加原理是正确的, 是一条必不可少的基本原理, 至少在微观世界中是如此. 一个电子确实可以“同时位于两个地方”。
关于量子叠加态的你同时在北京喝茶与四川打麻将，其实可以更直观地在后面的 双缝干涉实验 中被观察到。

下图是量子力学中常用的符号，在学习一系列有关运算与性质之前需要进行熟悉。

对最后两个线性代数中的知识进行简要介绍：
Hermite阵==埃尔米特
例：

内积：在量子力学中, 我们把态矢量 和它自身的内积记为
需要注意的是：量子力学中叠加态的各个系数, 通常是一个复数

态矢量内积的性质

本征态（eigen state)：对于某个物理量p（如位置，速度），在经典物理中可能被测量到的状态，称为本征态（现实中能观测到的物理量），不同的本征态往往是正交的
与线性代数中的知识相类比：本征态对应特征向量a，本征值对应特征值，态矢量对应矩阵
Aa=ra

态空间：由本征态作为基底，所有可能叠加态的集合
下图是两个正交的本征态下的态空间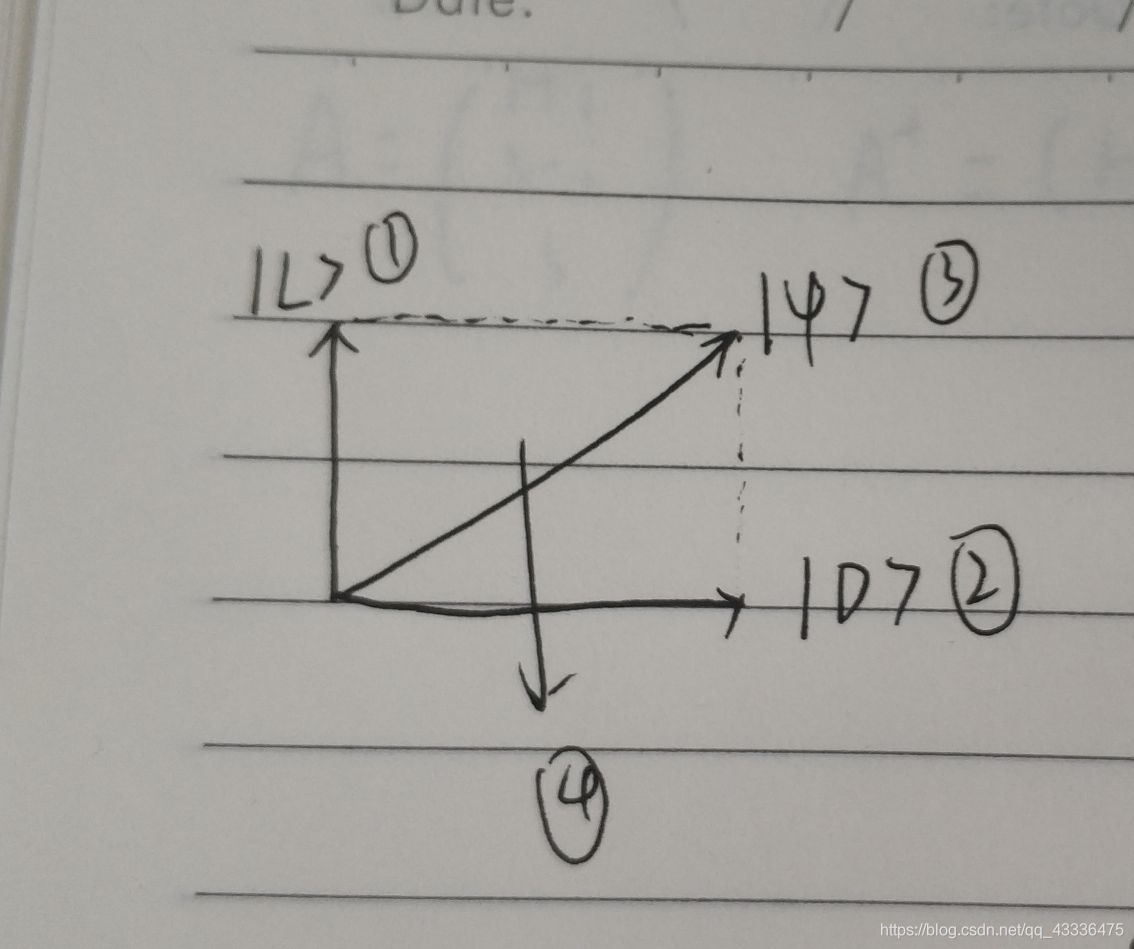

①②本征态 ③叠加态 ④态空间

坍缩:对态矢量进行测量之后，会从叠加态坍缩为一个确切的本征态。

测量是量子态上唯一不可逆的操作
如：在Stern-Gerlach实验中，测量银原子z方向自旋时，会坍缩至+ 或 z-,再次进行同样的z方向自旋测量，会发现原本坍缩至z+的依然是z+，原本坍缩至z-的依然是z-。这就是不可逆的操作。

张量积定义：
下面从一个例子来进一步理解张量积

这显然为我们打破了传统矩阵乘法中第一个矩阵的列数和下一个矩阵行数相同才能相乘的限制壁垒，也就是不拘束于Anm * Bml这种形式了。

量子纠缠态定义：当量子比特的叠加状态无法用各量子比特的张量乘积表示时, 这种叠加态就称为量子纠缠态。
纠缠态如:
由于它不能被分离为单个电子的态的乘积, 所以这个系统的态被称为纠缠态。
非纠缠态如：
可以“提取公因式”, 那么此态并不属于纠缠态。
量子态纠缠的直观理解：如果一个没有自旋的粒子衰变成两个电子, 纠错态就会出现. 由于角动量守恒, 两个电子的自旋必须是反向对齐的. 在经典物理中, 该系统则必须处于态|↑ ↓⟩或|↓↑⟩, 但在量子物理中, 它可以处于态|↑↓⟩和|↓↑⟩之间. 然后我们将这两个电子分开, 比如一个留在地球上, 另一个则被送往宇宙的另一端. 接着我们测量留在地球上的电子的自旋, 测量的结果有 50%的可能自旋向上, 50%的可能自旋向下。
但是, 一旦我们测得这个电子的自旋, 就能即刻确定在宇宙另一端的电子的自旋, 这也就是纠缠的奇妙之处。

量子逻辑门

单量子逻辑门
①泡利-X 门(Pauli-X gate)：

也即是对应经典逻辑非门。

②泡利-Y 门(Pauli-Y gate)：

③泡利-Z 门(Pauli-Z gate)：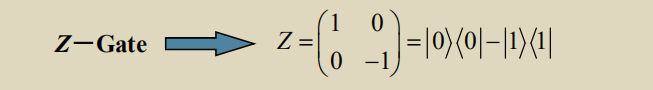

保留基本状态|0〉不变并且将|1〉换成-|1〉
④阿达马门(Hadamard Gate)

Hadamard 门 将 基 矢 |0〉和 |1〉 分 别 变 成
|+〉=（√1/2）( |0〉+ |1〉)和|-〉=（√1/2）( |0〉- |1〉)
即 0 和 1 的均匀叠加态, 系统等概率地(以 1/2 的概率)处 于 0 和 1 态。

双量子逻辑门
①受控非门 CNOT(Control-NOT gate)
定义受控非门可以操作两个量子比特, 其中, 第二个量子比特只有在第一个量子比特为 |1〉的时候才可以进行 NOT 操作, 否则整个双量子态就保持不变。

②受控互换门 SWAP(Swap gate)
互换门的操作对象也是两个量子比特, 其主要作用是交换两个量子比特的量子位。
|0，1〉切换为|1，0〉

③量子旋转门

用于对任意的叠加态进行旋转变换。

三量子逻辑门
Toffoli 门 CCNOT(Controlled-Controlled-NOT gate)
Toffoli 门是一个操作三个量子比特的的量子逻辑门，如果前两个量子比特是 |1〉, 则对第三个量子比特进行类似于经典的逻辑非门处理, 反之则整个三量子态不做操作。

量子门操作与并行计算

众所周知，传统计算机的并行执行只是宏观上的并行，在微观上来看，其实是每个进程不断切换共享使用计算机资源，并没有完全做到并行计算。但量子计算机就从根本上解决了这个问题。接下来将用几个例子来说明。
①
由于某些公式、符号写入过于麻烦，改为手写

量子寄存器与量子状态叠加
十进制数 10 和 5, 若用量子比特来表示, 取它们的叠加态,即为：

叠加态的定义为：

由此可见, 量子叠加状态是实现真正物理意义上并行计算的物质基础。

量子寄存器：量子寄存器就是量子比特的集合, 它是位串, 其长度决定了它可以存储的信息量 在叠加时, 寄存器中的每个量子位是 0 和 1 的叠加, 因此, 长度为 n 个量子位的寄存器是所有2^n 个可能的用 n 位表示的长度量子位串的叠加, 换句话说, 长度为 n 的量子寄存器的状态空间是 n 位基向量的线性组合, 每个长度为 2 ^n, 故我们可以得到：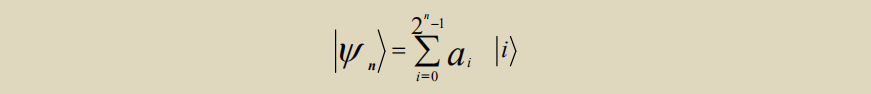

不确定性原理

不能通过测量同时确定两个不对易的物理量, 比如位置和动量, 因为对其中一个的测量行为会干扰被测对象的状态, 导致另一个物理量无法确定。
如：知道一个粒子的位置 x, 那么就完全无法确定它的动量 p

对易和反对易：算符 A 和 B 如果满足条件 AB=BA, 则称为对易的；如果 AB=-BA , 则称为反对易的。

对易子和反对易子:
量子算符的对易子定义为：[A,B]=AB-BA
对易关系即[A, B]=0；反对易子的定义为{A, B}=AB + BA, 反对易关系即{A, B}=0.

使用Quantum糖进一步理解不确定性原理

(1) 神奇 Q(quantum)糖
假设盒子里面有一颗Q糖，他不是一颗普通的糖，它的不普通就在于其味道有时甜, 有时酸；它的颜色有时红, 有时蓝。这里的“有时”需要特别注意，说的不是时间上的有时，而是每次“观测”之后的时候。你看他一眼，他可能是红色，也可能是蓝色，但不管是哪种颜色，只要你看到了，他就不再变化。我们不如假设他是蓝色吧，这时候你迫切地想要品尝他的味道，放到嘴里，很酸！拿出来再一看，竟然变成了红色，再放到嘴里，很甜！
经过多次试验你发现，并不是说蓝色就代表酸，红色就代表甜，也不是每次放到嘴里都会改变味道，也不是每次拿出来看一眼都会变色。他们之间似乎并没有什么联系。唯一可以确定的就是，如果他的味道你已经知道了，再怎么去尝，味道也不会变；如果他的颜色你已经看到了，再怎么看，他的颜色也不会改变。
(2) 线性代数复习课：基底变换
为了更好地说清楚这件事，我们可以先回顾一下线性代数中的线性组合。用b1，b2代表口味，a1,a2代表颜色
我们可以用其中一组基底|b1〉,|b2〉的线性组合来表示另外一组基底|a1〉,|a2〉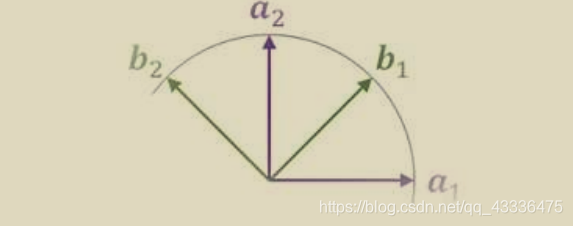
用代数式写为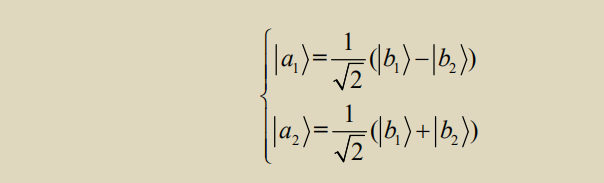

(3) 神奇 Q 糖的数学解释
当我们去观测他的颜色的时候，这个Q糖的量子态会由叠加态坍缩至|a1〉或者|a2〉其中一个本征态上，由于观测的不可逆性，此时无论再怎么继续观测，颜色也不会改变
但由于，|a1〉，|a2〉可以由|b1〉,|b 2〉的线性组合表示，所以味道（|b1〉,|b 2〉）这个属性是不确定的，换句话说就是Q糖的味道处于|b1〉,|b 2〉的量子叠加态中。此时我们在去品尝他的味道，就会坍缩至甜或酸，而此时颜色就处于量子叠加态中了。

所以就再次解释了不确定性原理：对于不对易的两个物理量，因为对其中一个的测量行为会干扰被测对象的状态, 导致另一个物理量无法确定。

恐怖的双缝干涉实验：

在19世纪的开头，英国物理学家托马斯杨就观测到将光束照射于两条相互平行的狭缝，在探射屏显示出一系列明亮条纹与暗淡条纹相间的图样。要知道干涉衍射是波所独有性质，而这显然的结果，使得波动说获得了空前的鼓舞。理解经典的杨氏干涉其实很简单，就是从两个缝射出的波，其振幅和相位在空间上的分布不同，相位相同的区域振幅相加呈现亮条纹，相位差的区域振幅相减呈现暗条纹。就有一点像从平静的水面上两个不同的点进行拍打，水波冲撞在一起导致的新的波纹。重叠的区域越多，表现出来的就是光斑越明亮
为了更好地理解这个实验，我们分解为三个实验逐步理解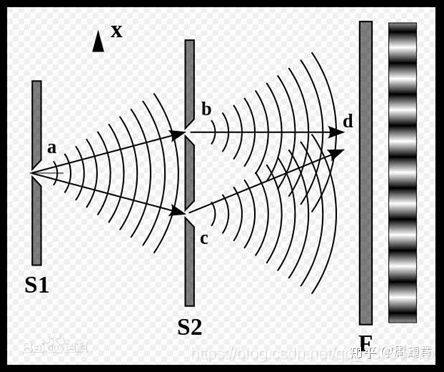

①：我们用一个光源连续的放出光子，把两个狭缝（b, c）都打开，那么在屏幕上会得到什么样的结果？
答：会得到和杨氏双缝一样的结果，在屏幕呈现一列列明暗相间的干涉条纹。
②：我们这时光源每次只放出一个光子，把两个狭缝（b, c）都打开，那么在屏幕上会得到什么样的结果？
答：这时，我们自然而然的会想到每次只有一个光子 ，光子不是从b狭缝通过就是从c狭缝通过，那么自然不可能会出现干涉现象，但是事实真的如此吗？结果却让人大跌眼镜：虽然每次只发射一个光子，但是经过一段时间的积累，还是出现了干涉条纹。这太让人费解了，明明两个狭缝只有一个狭缝有光子。那这个光子是和谁在进行干涉呢？难不成是和它自己的干涉吗？
实际上却是如此，由于这个光子处于一个叠加态中，所以他既从b狭缝通过又从c狭缝通过，由此而形成了干涉现象。
③：源每次只放出一个光子，把两个狭缝（b, c）都打开，但是在狭缝处放置光电探测器，就是说我能观测每个光子从哪个狭缝走，那么在屏幕上会得到什么样的结果？
答案是：干涉图样消失了！变成了两道简单的光束。这里我要引出本回答中第二个要强调的概念：测量。测量对于量子力学的意义就是—测量会引发叠加态的坍缩。之前的讨论中，我们说实验2的光子处于既从b狭缝通过，也从c狭缝通过的叠加态中，而实验3中的光子因为被在狭缝处被测量了，所以这个包含两个路径的叠加态一定会坍缩成只包含一个路径的单态，那这时这种基于叠加态的干涉就完全地被测量这一行为破坏掉了！

从双缝干涉实验中，就可以清晰地看到叠加态既在北京喝茶又在四川打麻将这一反常现象，同时也伸引测量与坍缩这两个重要概念。

本次博客的内容就到这里了。到目前为止，量子力学的内容依然让我兴致勃勃，希望可以尽快入门这个富有潜力的学科！