机器学习基础——主成分分析

主成分分析主成分分析（Principal Component Analysis,PCA）是最常用的一种降维方法。对于正交属性空间中的样本点，如果用一个超平面对所有的样本进行恰当的表达最近重构性：样本点到这个超平面的距离都足够近最大可分性：样本点在这个超平面上的投影能尽可能分开。假定数据样本进行中心化，即∑ixi=0\sum_i x_i=0∑ixi=0，在假定投影百年换后得到的新的...

绝尘花遗落

537人浏览 · 2019-09-20 20:45:10

绝尘花遗落 · 2019-09-20 20:45:10 发布

主成分分析

主成分分析（Principal Component Analysis,PCA）是最常用的一种降维方法。

对于正交属性空间中的样本点，如果用一个超平面对所有的样本进行恰当的表达

最近重构性：样本点到这个超平面的距离都足够近
最大可分性：样本点在这个超平面上的投影能尽可能分开。

假定数据样本进行中心化，即 $∑ixi=0\sum_i x_i=0$ ，在假定投影百年换后得到的新的坐标为 $,ωd}\{\omega_1,\omega_2,\cdots, \omega_d\}$ ，其中 $w_i$ 是标准正交基， $∣∣wi∣∣2=1,ωiTωj=0(i≠j)||w_i||_2=1,\omega_i^T\omega_j=0(i\ne j)$ ，若丢弃新坐标系中的部分坐标，即将维度降到 $d^{'} < d$ ，则样本点 $x_i$ 在低维坐标系中的投影是 $,zid′)z_i=(z_{i1},z_{i2},\cdots,z_{id^{'}})$ ，其中 $zij=ωjTxiz_{ij}=\omega^T_jx_i$ 是 $x_i$ 在低维坐标系下第j维的坐标，若基于 $z_i$ 来重构 $x_i$ ，就会得到 $x^i=∑j=1d′zijwj\hat{x}_i = \sum_{j=1}^{d^{'}} z_{ij}w_j$

考虑整个训练集，原样本点 $x_i$ 是基于投影重构的样本点 $x^i\hat{x}_i$ 之间的距离为
$\sum_{i=1}^m ||\sum_{j=1}^{d^{'}} z_{ij}\omega -x_i||_2^2 = \sum_{i=1}^m z_i^Tz_i-2\sum_{i=1}^m z_i^TW^Tx_i+const \\ \varpropto -tr(W^T(\sum_{i=1}^m x_ix_i^T)W)$
已知 $W^TW=I,z_i = W^Tx_i$
$\begin{aligned} \sum_{i=1}^m ||\sum_{j=1}^{d^{'}}z_{ij}w_j-x_i||_2^2 & = \sum_{i=1}^m ||Wz_i-x_i||^2_2 \\ & = \sum_{i=1}^m(Wz_i-x_i)^T(Wz_i-x_i) \\ &= \sum_{i=1}^m (z_i^TW^TWz_i-z_i^TW^Tx_i-x_i^TWz_i+x_i^Tx_i)\\ &= \sum_{i=1}^m (z_i^Tz_i-2z_i^TW^Tx_i+x_i^Tx_i)\\ &=\sum_{i=1}^m z_i^Tz_i - 2\sum_{i=1}^m z_i^TW^Tx_i + \sum_{i=1}^m x_i^Tx_i\\ &= \sum_{i=1}^m z_i^Tz_i -2\sum_{i=1}^m z_i^Tz_i + const \\ &= -\sum_{i=1}^m z_i^Tz_i + const \\ &= -\sum_{i=1}^m tr(z_iz_i^T) +const\\ &= -tr(\sum_{i=1}^m W^Tx_ix_i^TW) + const \\ &= -tr(W^T(\sum_{i=1}^m x_ix_i^T)W) + const \end{aligned}$
根据最近重构性，上式应该被最小化，考虑到 $w_j$ 是标准正交基 $∑ixixiT\sum_{i}x_ix_i^T$ 是协方差矩阵
$\underset{W}{\min} -tr(W^TXX^TW) \\ s.t. \ W^TW =1$
这就是主成分分析的优化目标

从最大可分性出发，得到主成分分析的另外一种解释，样本点 $x_i$ 在新空间中超平面上的投影是 $W^Tx_i$ ，若所有样本点的投影能尽可能分开，应该使投影后样本点的方差最大化。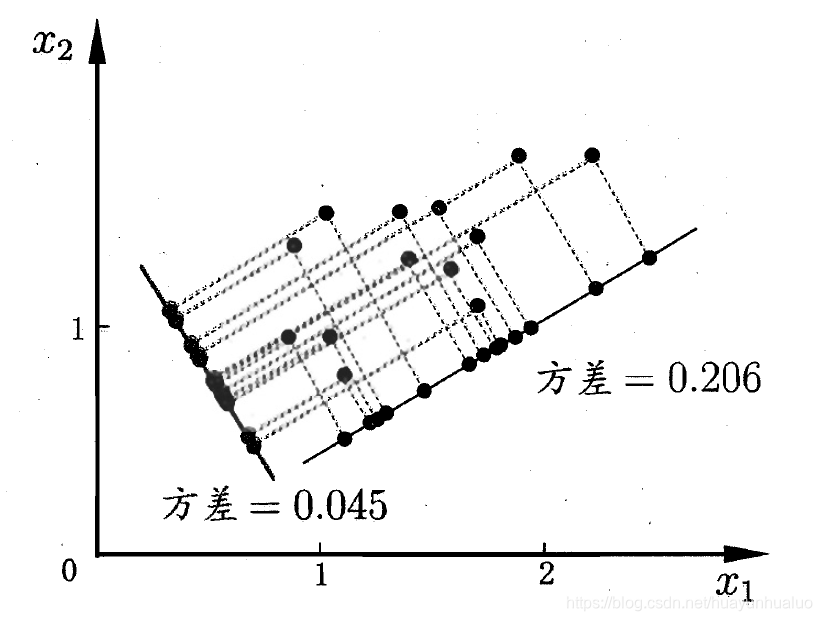
在这里插入图片描述

于是优化目标可写为：
$\underset{W}{\max} \ tr (W^TXX^TW) \\ s.t. \ W^TW=I$
使用拉格朗日乘子法可得
$XX^TW = \lambda W$
推导

$,wd′)∈Rd×d′,I∈Rd′×d′X=(x_1,x_2,\cdots,x_m)\in \mathbb{R}^{d\times m},W=(w_1,w_2,\cdots,w_{d^{'}})\in \mathbb{R}^{d\times d^{'}},I\in \mathbb{R}^{d^{'}\times d^{'}}$ 为单位矩阵，对于带矩阵约束的优化问题，优化目标的拉格朗日函数为
$\begin{aligned} L(W,\Theta) &= -tr(W^TXX^TW) + \langle \Theta,W^TW-I \rangle \\ &= -tr(W^TXX^TW) + tr(\Theta^T(W^TW-I)) \end{aligned}$
其中， $Θ∈Rd′×d′\Theta\in \mathbb{R}^{d^{'}\times d^{'}}$ 为拉格朗日乘子矩阵，其维度恒等于约束条件的维度，且其中的每个元素均为未知的拉格朗日乘子。若此时只考虑约束 $,d′)||w_i||_2 = 1(i=1,2,\cdots,d^{'})$ ，则拉格朗日乘子矩阵 $Θ\Theta$ 此时为对角矩阵，令新的拉格朗日乘子矩阵为 $,λd′)∈Rd′×d′\Lambda=diag(\lambda_1,\lambda_2,\cdots,\lambda_{d^{'}})\in \mathbb{R}^{d^{'}\times d^{'}}$ ,新的拉格朗日函数为
$L(W,\Lambda) = -tr(W^TXX^TW) + tr(\Lambda^T(W^TW-I))$
对拉格朗日函数关于 $W$ 求导可得
$\begin{aligned} \frac{\partial L(W,\Lambda)}{\partial W} & = \frac{\partial}{\partial W}[-tr(W^TXX^TW) + tr(\Lambda^T(W^TW-I))] \\ &= -\frac{\partial}{\partial W}tr(W^TXX^TW) + \frac{\partial}{\partial W}tr(\Lambda^T(W^TW-I)) \end{aligned}$
由矩阵微分公式 $∂∂Xtr(XTBX)=BX+BTX,∂∂Xtr(BXTX)=XBT+XB\frac{\partial}{\partial X}tr(X^TBX) = BX+B^TX,\frac{\partial}{\partial X} tr(BX^TX) = XB^T+XB$
$\begin{aligned} \frac{\partial L(W,\Lambda)}{\partial W} &= -2XX^TW +W\Lambda + W\Lambda^T \\ &=-2XX^TW+W(\Lambda + \Lambda^T) \\ &= -2XX^TW + 2W\Lambda \end{aligned}$
令 $∂L(W,Λ)∂W=0\frac{\partial L(W,\Lambda)}{\partial W}=0$
$-2XX^TW +2W\Lambda = 0\\ XX^TW = W\Lambda$
只需要对协方差矩阵 $XX^T$ 进行特征值分解，将求得的特征值排序 $λ1≥λ2⋯≥λd\lambda_1 \ge \lambda_2 \cdots \ge \lambda_d$ ，再取前 $d^{'}$ 个特征值对应的特征值对应的特征向量构成 $,ωd′)W=(\omega_1,\omega_2\cdots, \omega_{d^{'}})$

算法步骤：

输入：样本集 $,xm}D=\{x_1,x_2,\cdots,x_m\}$ ，低维空间维数 $d^{'}$
过程：
1. 对所有样本进行中心化 $xi←xi−1m∑i=1mxix_i \leftarrow x_i-\frac{1}{m}\sum_{i=1}^m x_i$
2. 计算样本的协方差矩阵 $XX^T$
3. 对协方差矩阵 $XX^T$ 做特征值分解
4. 取最大的 $d^{'}$ 个特征值所对应的特征向量 $,wd′w_1,w_2,\cdots,w_{d^{'}}$
输出：投影矩阵

降维后的低维空间的维数 $d^{'}$ 通常是由用户先指定，或通过在 $d^{'}$ 值不同的低维空间中对 $k$ 近邻分类器进行交叉验证来选择较好的 $d^{'}$ 值。
$\frac{\sum_{i=1}^{d^{'}}\lambda_i}{\sum_{i=1}^d \lambda_i} \ge t$
PCA仅需保留W与样本的均值向量即可通过简单的向量减法和矩阵-向量乘法将新的样本投影到低维空间中，因为对应于最小的 $d-d^{'}$ 个特征值的特征向量被舍弃了，这就是降维导致的结果。但是舍弃这部分往往是必要的：