人工智能学习笔记3：贝叶斯决策理论part 2（最大似然数估计ML）
上一部分讲了贝叶斯决策的基本概念和使用它来做分类器（判别函数、决策面）接下来引入最大似然估计和贝叶斯参数估计每个样本集中的样本都是所谓 独立 同分布的随机变量【任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立，那么这些随机变量是独立同分布。】，且有充分 的训练样本类的条件概率密度估计（非常难），可分为这两类说到那么难的一个问题，所以我们本章的重点就是：试试用最大似然数估计解决
·
上一部分讲了贝叶斯决策的基本概念和使用它来做分类器（判别函数、决策面）
接下来引入
最大似然估计和贝叶斯参数估计
每个样本集中的样本都是所谓 独立 同分布的随机变量【任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立，那么这些随机变量是独立同分布。】，且有充分 的训练样本
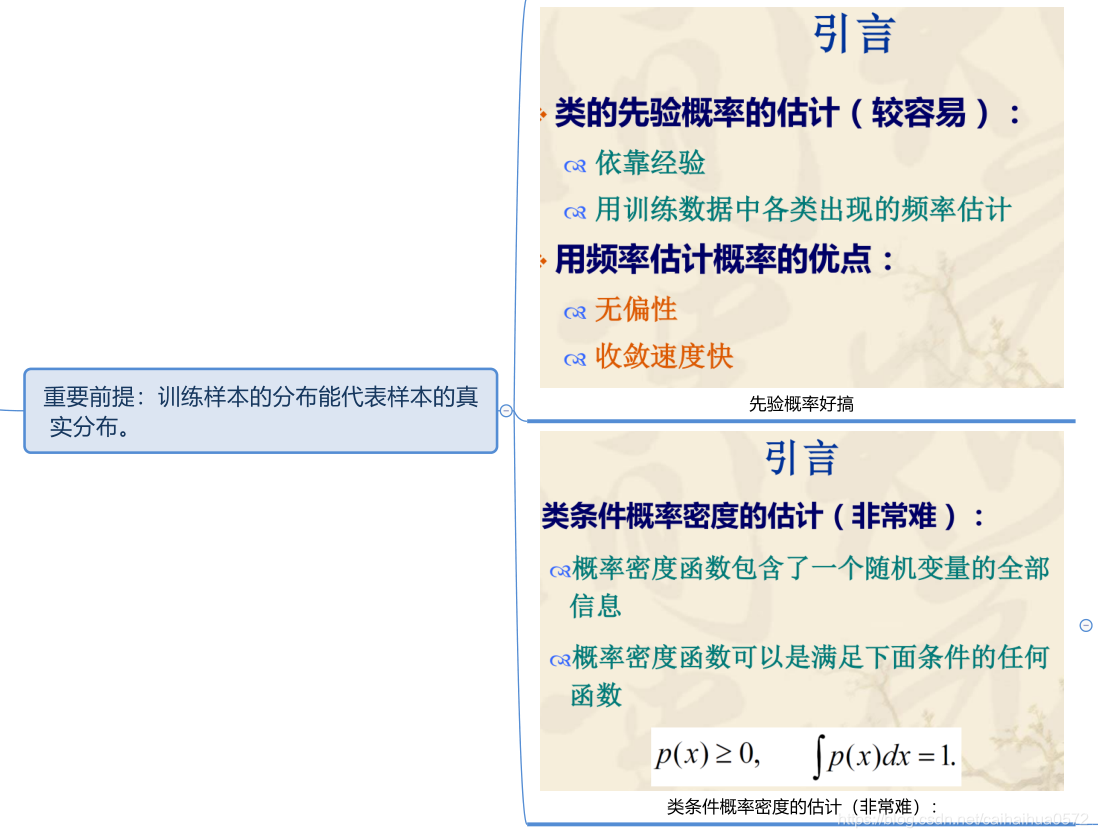
类的条件概率密度估计（非常难），可分为这两类
说到那么难的一个问题，所以我们本章的重点就是：
试试用最大似然数估计解决这个问题
初始化一下条件
单个参数ML估计
介绍一下那个未知参数的含义
要解决的问题：
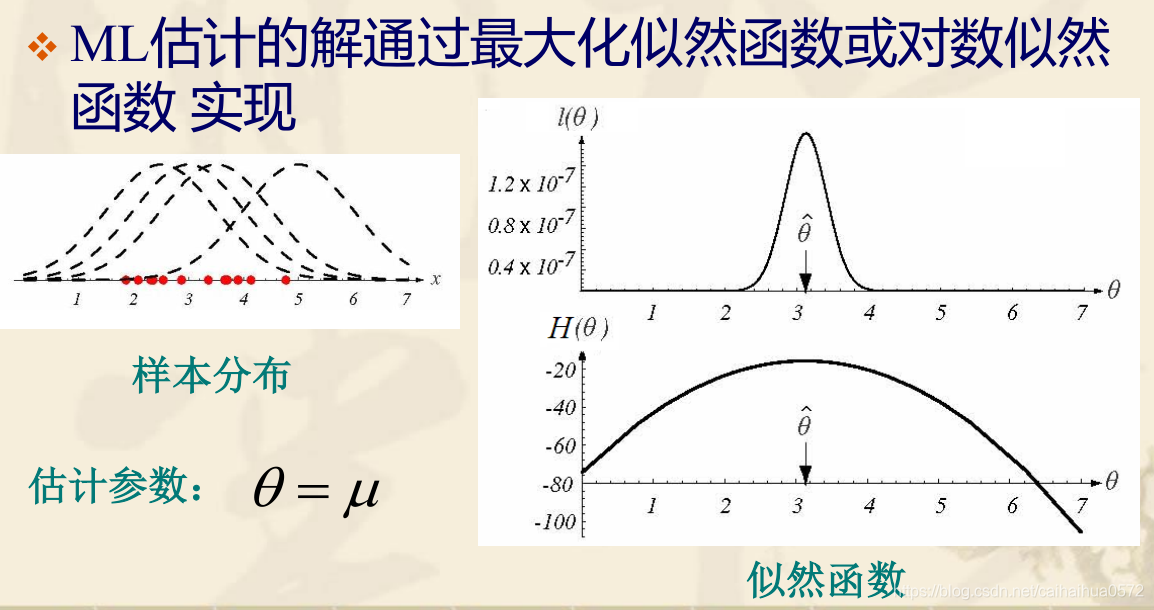
ML的求解：
多个参数情况下ML估计
唯一解情况
其他情况
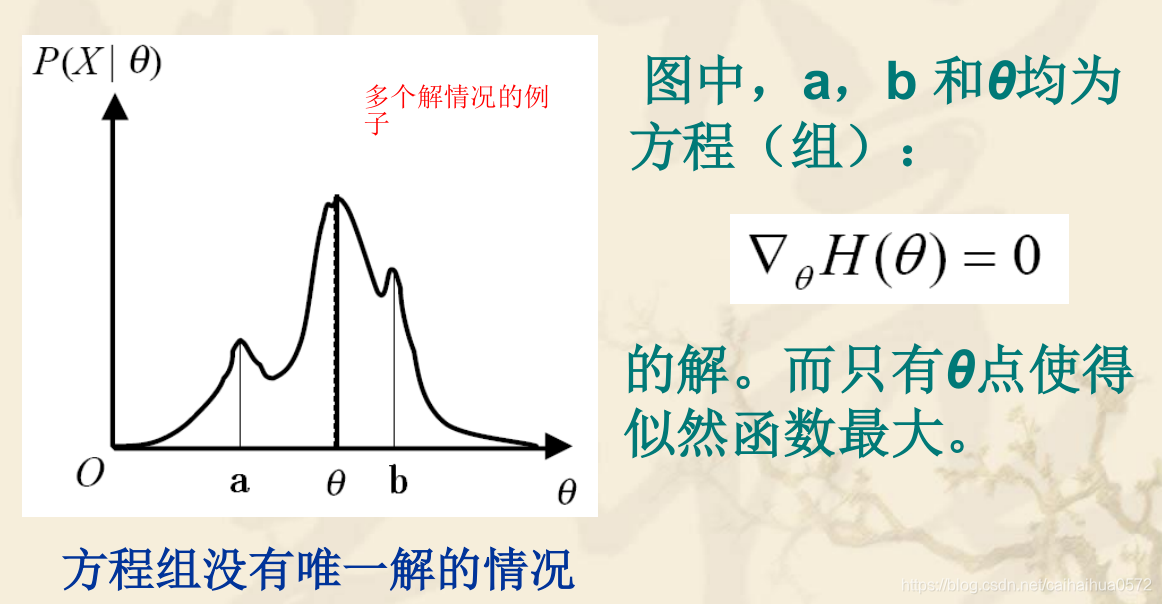
无法求解的情况：均匀分布
正态分布情况分析
最后解得
汇聚全球AI编程工具，助力开发者即刻编程。
更多推荐
0
0- 0
已为社区贡献1条内容
所有评论(0)